题目内容
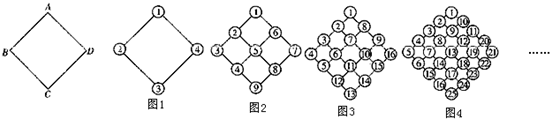
如图,将菱形ABCD的每条边1,2,3,…,n,…等分,并按图1,图2,图3,;图4,…的方式连结等分点,将每个点依图示规律填上1,2,3,4,5,6,…,例如图3中菱形ABCD的四个顶点上所填数字之和为34.
(1)图5中,菱形ABCD的四个顶点上所填数字之和是 ;
(2)图n中,菱形ABCD的四个顶点上所填数字之和是 .

(1)图5中,菱形ABCD的四个顶点上所填数字之和是
(2)图n中,菱形ABCD的四个顶点上所填数字之和是
考点:归纳推理
专题:规律型
分析:由已知中的四个图形,分析A,B,C,D四个顶点上所填数字的变化规律,进而分析出菱形ABCD的四个顶点上所填数字之和的表达式,可得答案.
解答:
解:由第1图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,2,3,4,
由第2图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,3,7,9,
由第3图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,4,13,16,
由第4图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,5,21,25,
…
归纳可得:由第n图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,n+1,(n+1)2-n,(n+1)2,
故第n图形中,A,B,C,D四个顶点上所填数字之和为:1+n+1+(n+1)2-n+(n+1)2=2n2+4n+4,
当n=5时,2n2+4n+4=74
故答案为:(1)74;(2)2n2+4n+4
由第2图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,3,7,9,
由第3图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,4,13,16,
由第4图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,5,21,25,
…
归纳可得:由第n图形中,A,B,C,D四个顶点上所填数字从小到大分别为:1,n+1,(n+1)2-n,(n+1)2,
故第n图形中,A,B,C,D四个顶点上所填数字之和为:1+n+1+(n+1)2-n+(n+1)2=2n2+4n+4,
当n=5时,2n2+4n+4=74
故答案为:(1)74;(2)2n2+4n+4
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
若两个函数的图象仅经过若干次平移能够重合,则称这两个函数为“同形”函数,给出下列三个函数:f1(x)=2cos2x,f2(x)=sinx+
cosx,f3(x)=2cos(x-
)-1,则( )
| 3 |
| π |
| 3 |
| A、f1(x),f2(x),f3(x)两两为“同形”函数 |
| B、f1(x),f2(x),f3(x)两两不为“同形”函数 |
| C、f1(x),f2(x)为“同形”函数,且它们与f3(x) 不为“同形”函数 |
| D、f2(x),f3(x)为“同形”函数,且它们与f1(x) 不为“同形”函数 |
在等差数列{an}中,已知a2+a6=
,则sin(2a4+
)=( )
| π |
| 6 |
| π |
| 3 |
A、
| ||||
| B、0 | ||||
| C、-1 | ||||
| D、1 |
设集合A={1,2,3,4},B={2,3,5},则A∩B=( )
| A、{5} |
| B、{2,3} |
| C、{2,3,5} |
| D、{1,4,5} |