题目内容
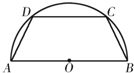 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设∠BAC=θ,作CE⊥AB于点E,则可表示出BC,EB,CD,进而可求得梯形的周长的表达式,根据二次函数的性质求得周长的最大值时θ的值,则AC和BC可求,进而根据双曲线的定义求得双曲线的长轴,
解答:
解:设∠BAC=θ,作CE⊥AB于点E,
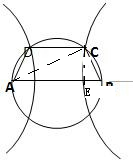
则BC=2Rsinθ,EB=BCcos(90°-θ)=2Rsin2θ,有CD=2R-4Rsin2θ,
梯形的周长l=AB+2BC+CD=2R+4Rsinθ+2R-4Rsin2=8+8sinθ-8sin2θ=-8(sinθ-
)2+10
当sinθ=
,即θ=30°时,l有最大值10,
∴BC=2,AC=2
,a=
(AC-BC)=
-1,
∴双曲线的实轴长为2a=2
-2
故选:D.

则BC=2Rsinθ,EB=BCcos(90°-θ)=2Rsin2θ,有CD=2R-4Rsin2θ,
梯形的周长l=AB+2BC+CD=2R+4Rsinθ+2R-4Rsin2=8+8sinθ-8sin2θ=-8(sinθ-
| 1 |
| 2 |
当sinθ=
| 1 |
| 2 |
∴BC=2,AC=2
| 3 |
| 1 |
| 2 |
| 3 |
∴双曲线的实轴长为2a=2
| 3 |
故选:D.
点评:本题主要考查了双曲线的应用,双曲线的定义.考查了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若两个函数的图象仅经过若干次平移能够重合,则称这两个函数为“同形”函数,给出下列三个函数:f1(x)=2cos2x,f2(x)=sinx+
cosx,f3(x)=2cos(x-
)-1,则( )
| 3 |
| π |
| 3 |
| A、f1(x),f2(x),f3(x)两两为“同形”函数 |
| B、f1(x),f2(x),f3(x)两两不为“同形”函数 |
| C、f1(x),f2(x)为“同形”函数,且它们与f3(x) 不为“同形”函数 |
| D、f2(x),f3(x)为“同形”函数,且它们与f1(x) 不为“同形”函数 |
数列{an}满足:a1=2,an+1=an+2(n∈N*),则其前10项的和S10=( )
| A、100 | B、101 |
| C、110 | D、111 |
设集合A={1,2,3,4},B={2,3,5},则A∩B=( )
| A、{5} |
| B、{2,3} |
| C、{2,3,5} |
| D、{1,4,5} |
以下有关线性回归分析的说法不正确的是( )
A、通过最小二乘法得到的线性回归直线经过样本的中心(
| ||||
B、用最小二乘法求回归直线方程,是寻求使
| ||||
| C、在回归分析中,变量间的关系若是非确定性关系,但因变量也能由自变量唯一确定 | ||||
| D、如果回归系数是负的,y的值随x的增大而减小 |
某堂训练课上,一射击运动员对同一目标独立地进行了四次射击,已知他至少命中一次的概率为
,则四次射击中,他命中2次的概率为( )
| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
观察下列各式:则31=3,32=9,33=27,…,则32014的个位数字为( )
| A、1 | B、3 | C、7 | D、9 |
复数
的共轭复数是( )
| 5 |
| 2i-1 |
| A、2i+1 | B、-1-2i |
| C、2i-1 | D、1-2i |
