题目内容
从1，2，3，4，5，6，7中选出三个互不相邻的数，选法有 种．（填数字）
考点：计数原理的应用
专题：排列组合
分析：根据题意，按照取出数字的大小，从小到大排列，分3种情况讨论，由分类加法原理计算可得答案
解答：
解：因为是组合问题，不必考虑顺序，则按照取出数字的大小，从小到大排列，分3种情况讨论：
①、数字1开头的取法有135、136、137、146，147，157共有6种．
②、数字2开头的取法有246、247、257共有3种．
③、数字3开头的取法有357共有1种．
综上，这三个数互不相邻的取法种数有6+3+1=10种．
故答案为：10．
①、数字1开头的取法有135、136、137、146，147，157共有6种．
②、数字2开头的取法有246、247、257共有3种．
③、数字3开头的取法有357共有1种．
综上，这三个数互不相邻的取法种数有6+3+1=10种．
故答案为：10．
点评：本题考查分类计数原理，首先注意是组合问题，其次分类讨论要按一定的顺序、规律，做到不重不漏．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
若两个函数的图象仅经过若干次平移能够重合，则称这两个函数为“同形”函数，给出下列三个函数：f1（x）=2cos2x，f2（x）=sinx+
cosx，f3（x）=2cos（x-
）-1，则（ ）
| 3 |
| π |
| 3 |
| A、f1（x），f2（x），f3（x）两两为“同形”函数 |
| B、f1（x），f2（x），f3（x）两两不为“同形”函数 |
| C、f1（x），f2（x）为“同形”函数，且它们与f3（x） 不为“同形”函数 |
| D、f2（x），f3（x）为“同形”函数，且它们与f1（x） 不为“同形”函数 |
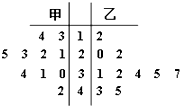从甲、乙两个城市分别随机抽取10台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示）．设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
半径为3，中心角为120°的扇形面积为（ ）
| A、4π2 |
| B、3π |
| C、6π |
| D、2π2 |
以下有关线性回归分析的说法不正确的是（ ）
A、通过最小二乘法得到的线性回归直线经过样本的中心（
| ||||
B、用最小二乘法求回归直线方程，是寻求使
| ||||
| C、在回归分析中，变量间的关系若是非确定性关系，但因变量也能由自变量唯一确定 | ||||
| D、如果回归系数是负的，y的值随x的增大而减小 |
