题目内容
在复数范围内，方程x2=-1的解是（ ）
| A、±1 | B、-1 | C、±i | D、i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：设x=a+bi，a，b∈R，可得（a+bi）2=-1，由复数相等可得a和b方程组，解方程组可得．
解答：
解：设x=a+bi，a，b∈R，
∵x2=-1，∴（a+bi）2=-1，
∴a2-b2+2abi=-1，
∴
，
解得
，
∴x=±i
故选：C
∵x2=-1，∴（a+bi）2=-1，
∴a2-b2+2abi=-1，
∴
|
解得
|
∴x=±i
故选：C
点评：本题考查复数的代数形式的运算，属基础题．
练习册系列答案
相关题目
若两个函数的图象仅经过若干次平移能够重合，则称这两个函数为“同形”函数，给出下列三个函数：f1（x）=2cos2x，f2（x）=sinx+
cosx，f3（x）=2cos（x-
）-1，则（ ）
| 3 |
| π |
| 3 |
| A、f1（x），f2（x），f3（x）两两为“同形”函数 |
| B、f1（x），f2（x），f3（x）两两不为“同形”函数 |
| C、f1（x），f2（x）为“同形”函数，且它们与f3（x） 不为“同形”函数 |
| D、f2（x），f3（x）为“同形”函数，且它们与f1（x） 不为“同形”函数 |
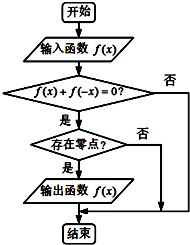
某流程图如图所示，以下四个选项中哪一个函数输入后能够被输出（ ）
| A、f（x）=ex-e-x | ||
| B、f（x）=x2-2 | ||
C、f（x）=
| ||
| D、f（x）=lgsinx |
在等差数列{an}中，已知a2+a6=
，则sin（2a4+
）=（ ）
| π |
| 6 |
| π |
| 3 |
A、
| ||||
| B、0 | ||||
| C、-1 | ||||
| D、1 |
若离散型随机变量X的分布列如下表，则a=（ ）
| X | 0 | 1 |
| P | 2a | 0.6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某堂训练课上，一射击运动员对同一目标独立地进行了四次射击，已知他至少命中一次的概率为
，则四次射击中，他命中2次的概率为（ ）
| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |