题目内容
10.已知△ABC,$A({1,1}),B({1,3}),C({1+\sqrt{3},2})$,若点(x,y)在三角形内部(不包含边界),则z=-2x+y的取值范围是( )| A. | $({-\sqrt{3},-1})$ | B. | (-1,1) | C. | $({-2\sqrt{3},1})$ | D. | $({-1,\sqrt{3}})$ |
分析 作出平面区域,利用目标函数的几何意义,利用数形结合进行求解即可.
解答 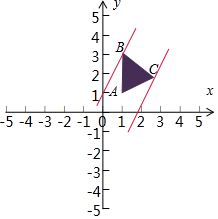 解:由y=2x+z,
解:由y=2x+z,
作出不等式组对应的平面区域如图(阴影部分ABC)
平移直线y=2x+z,由图象可知当直线y=2x+z,过点B时,直线y=2x+z截距最大,此时z最大,
代入目标函数z=-2x+y,
得z=-2×1+3=1.
∴目标函数z=-2x+y的最大值是1.
过点C时,直线y=-2x+z截距最小,此时z最小,
代入目标函数z=2x+y,
得z=-2×(1+$\sqrt{3}$)-2=-2$\sqrt{3}$,
∴目标函数z=-2x+y的最小值是-2$\sqrt{3}$.
故z的取值范围是(-2$\sqrt{3}$,1).
故选:C.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
18.已知△ABC中,a=4$\sqrt{2}$,b=4,A=45°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
5.某校有“交通志愿者”和“传统文化宣讲”两个社团,若甲、乙、丙三名学生各自随机选择参加其中一个社团,则三人不在同一个社团的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{8}$ |
15.已知直线m,n均在平面α内,则“直线l⊥m且直线l⊥n”是“直线l⊥平面α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.已知集合A={x|x2-x+a=0}的子集有4个,则实数a的取值范围为( )
| A. | $({\frac{1}{4},+∞})$ | B. | $[{\frac{1}{4},+∞})$ | C. | $({-∞,\frac{1}{4}})$ | D. | $({-∞,\frac{1}{4}}]$ |