题目内容
9.若直线l沿x轴向左平移4个单位,再沿y轴向上平移1个单位后,回到原来的位置,则直线l的斜率是-$\frac{1}{4}$.分析 设直线l的方程为:y=kx+b,由已知可得kx+b=k(x+4)+b+1,解得答案.
解答 解:设直线l的斜率为k,
直线l的方程为:y=kx+b,
则直线l沿x轴向左平移4个单位,再沿y轴向上平移1个单位后,
函数的解析式为:y=k(x+4)+b+1,
由题意得:kx+b=k(x+4)+b+1,
解得:k=-$\frac{1}{4}$,
故答案为:-$\frac{1}{4}$
点评 本题考查的知识点是函数图象的平移变换,多项式相等的充要条件,难度中档.

练习册系列答案
相关题目
4.若集合M={x|y=loga(1-x2)},N={y|y=x2+1,x∈R},则∁R(M∪N)( )
| A. | (-∞,-1] | B. | (-1,+∞) | C. | (-1,1) | D. | [1,+∞) |
14.正在进行中的CBA比赛吸引了众多观众,辽篮的表现更是牵动了广大球迷的心,某机构为了解该地群众对赛事的关注程度,随机调查了120名群众,得到如下列联表(单位:名)
附表:
${K^2}=\frac{{n{{(ad-cb)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)从这80名男群众中按是否对赛事关注分层抽样,抽取一个容量为8的样本,问样本中对赛事关注和不关注的群众各多少名?
(2)根据以上列联表,问能否在犯错率不超过0.010的前提下认为群众性别与关注赛事有关?
(3)从(1)中的8名男性群众中随机选取2名进行跟踪调查,求选到的两名群众中恰有一名观注赛事的概率.
| 男 | 女 | 合计 | |
| 关注 | 60 | 20 | 80 |
| 不关注 | 20 | 20 | 40 |
| 合计 | 80 | 40 | 120 |
| p(k2≥k0) | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)从这80名男群众中按是否对赛事关注分层抽样,抽取一个容量为8的样本,问样本中对赛事关注和不关注的群众各多少名?
(2)根据以上列联表,问能否在犯错率不超过0.010的前提下认为群众性别与关注赛事有关?
(3)从(1)中的8名男性群众中随机选取2名进行跟踪调查,求选到的两名群众中恰有一名观注赛事的概率.
18.已知△ABC中,a=4$\sqrt{2}$,b=4,A=45°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
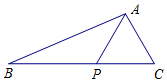 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.