题目内容
18.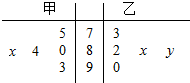 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
分析 先由甲同学所得评分的众数为84,则80+x=84,即x=4,再分别求出甲,乙的平均数,根据条件得到y的范围,根据概率公式计算即可.
解答 解:由茎叶图可知,甲的评分得分为:75,80,84,80+x,93,
乙的评分得分为:73,82,80+x,80+y,90,
由甲同学所得评分的众数为84,则80+x=84,即x=4,
甲的平均分为$\frac{1}{5}$×(75+80+84+84+93)=83.2,
乙的平均分为$\frac{1}{5}$×(73+82+84+80+y+90)=81.8+$\frac{y}{5}$,
∵甲同学所得评分的平均数不大于乙同学所得评分的平均数,
∴83.2≤81.8+$\frac{y}{5}$,
解得y≥7,
∵0≤y<10
∴甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为$\frac{10-7}{10}$=$\frac{3}{10}$,
故选:A.
点评 本题考查了茎叶图的知识,以及平均数,众数的问题,以及几何概型概率的问题,属于基础题.

练习册系列答案
相关题目
8.已知a,b,c为非零常数,则下列命题正确的是( )
| A. | 若a<b,则a2<b2 | B. | 若a<b,则ac<bc | C. | 若a>b,则ac2>bc2 | D. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ |
13.“x≠1”是“x2+2x-3≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
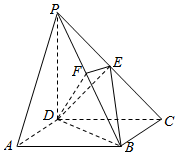 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.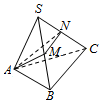 如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值.
如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,∠ASB=30°,M、N分别为棱SB和SC上的点,求△AMN的周长的最小值. 在空间四边形ABCD中,E、F、O、H分别是AB、BC、CD、DA的中点,且AC=BD,求证:EO与FH互相垂直平分.
在空间四边形ABCD中,E、F、O、H分别是AB、BC、CD、DA的中点,且AC=BD,求证:EO与FH互相垂直平分.