题目内容
14．若f（x）=ex-kx的极小值为0，则k=e．分析 先求出函数的导数，得到f（x）在x=lnk处取得极小值0，解方程elnk-klnk=0即可．
解答 解：f′（x）=ex-k，若f（x）有极小值，则k＞0，
令f′（x）＞0，解得：x＞lnk，令f′（x）＜0，解得：x＜lnk，
∴f（x）在x=lnk处取得极小值0，
故f（lnk）=elnk-klnk=0，解得：k=e，
故答案为：e．
点评 本题考查了函数的极值、导数的应用问题，考查学生的计算能力，是一道基础题．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
4．设全集U=R，集合A={1，3，5，7}，B={x|3＜x＜7}，则A∩（∁UB）=（ ）
| A． | {1，3，5} | B． | {1，3，7} | C． | {5} | D． | {1} |
5．已知a，b是两条直线，α是一个平面，则下列判断正确的是（ ）
| A． | a⊥α，b⊥α，则a⊥b | B． | a∥α，b?α，则a∥b | ||
| C． | a⊥b，b?α，则a⊥α | D． | a∥α，b?α，a?α，则a∥α |
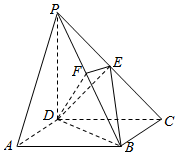如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，点E是PC的中点，作EF⊥PB交PB于点F．
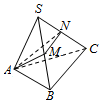如图，一个三棱锥，底面ABC为正三角形，侧棱SA=SB=SC=1，∠ASB=30°，M、N分别为棱SB和SC上的点，求△AMN的周长的最小值．