题目内容
14. 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.( I ) 求圆M和抛物线C的方程;
(Ⅱ) 已知点N是x轴正半轴上的一个定点,设G,H是抛物线上异于原点O的两个不同点,且$\overrightarrow{GN}$∥$\overrightarrow{NH}$,△GOH面积的最小值为16.问以动线段GH为直径的圆是否过原点?请说明理由.
分析 ( I )由抛物线C:y2=2px(p>0)的准线为l,即$\frac{p}{2}$=丨OA丨•cos60°=1,则p=2,即可求得抛物线C的方程,设圆的半径为r,则r=$\frac{丨OB丨}{2}$•$\frac{1}{cos60°}$=2,圆的方程为:(x-2)2+y2=4;
(Ⅱ)设GH的方程为:x=my+n,代入椭圆方程,y1+y2=4m,y1•y2=-4n,S△GOH=SGOH+SNOH=$\frac{1}{2}$•n•丨y1-y2丨=$\frac{1}{2}$•n•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}$•n•$\sqrt{16{m}^{2}+16n}$≥16,m=0时,S△GOH最小,此时n=4.由$\overrightarrow{OG}$•$\overrightarrow{OH}$=x1•x2+y1•y2=0,以线段GH为直径的圆过原点.
解答 解:(Ⅰ)由抛物线C:y2=2px(p>0)的准线为l,即$\frac{p}{2}$=丨OA丨•cos60°=1,则p=2,
∴抛物线的方程为y2=4x.…(2分)
由圆M的圆心在x轴的正半轴上,且与y轴相切,且|AO|=|OB|=2,
设圆的半径为r,则r=$\frac{丨OB丨}{2}$•$\frac{1}{cos60°}$=2,
故圆心M(2,0),
∴圆的方程为:(x-2)2+y2=4; …(4分)
(Ⅱ)设G(x1,y1),H(x2,y2),N(n,0)(n为大于0的常数).
设GH的方程为:x=my+n,
∴$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+n}\end{array}\right.$,整理得:y2-4my-4n=0,
∴y1+y2=4m,y1•y2=-4n
S△GOH=SGOH+SNOH=$\frac{1}{2}$•n•丨y1-y2丨=$\frac{1}{2}$•n•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$,
=$\frac{1}{2}$•n•$\sqrt{16{m}^{2}+16n}$≥16,
由n为大于0的常数,
∴m=0时,S△GOH最小.此时n=4. …(8分)
由$\overrightarrow{OG}$•$\overrightarrow{OH}$=x1•x2+y1•y2=0,
∴以线段GH为直径的圆过原点.…(12分)
点评 本题考查抛物线的标准方程及简单几何性质,考查直线与抛物线的位置关系,考查三角形面积公式,韦达定理及弦长公式的应用,考查圆锥曲线与不等式的综合应用,考查计算能力,属于中档题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
 为锐角,且
为锐角,且 ,则
,则 .
.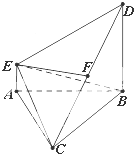 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
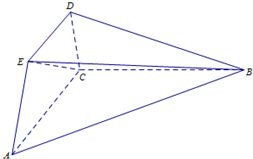 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.