题目内容
9.已知抛物线C:y2=4x,O是原点,A,B为抛物线上两动点,且满足OA⊥OB,若OM⊥AB于M点.(Ⅰ)求M的轨迹方程.
(Ⅱ)过点F(1,0)作互相垂直的两条直线l1,l2,分别交抛物线C于点P、Q和点K、L.设线段PQ,KL的中点分别为R、T,求证:直线RT恒过一个定点.
分析 (Ⅰ)设AB:x=my+n代入抛物线方程,由韦达定理可知:y1•y2=-4n,则16x1•x2=(y1•y2)2=16n2,由$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,y1y2+x1x2=0,n2-4n=0,而OM⊥AB,$m=\frac{y}{x}$,代入x=my+n,整理M的轨迹方程x2+y2-4x=0(x≠0);
(Ⅱ)显然直线斜率存在且不为0,由题意可设直线的方程为y=k(x-1)(k≠0),代入抛物线方程,△=(2k2+4)2-4k4=16k2+16>0,由韦达定理可知:x3+x4=2+$\frac{4}{{k}^{2}}$,则y3+y4=k(x3+x4-2)=$\frac{4}{k}$,利用中点坐标公式求得R和T点坐标,求得直线RT的方程,yk2+(x-3)k-y=0,直线RT恒过定点E(3,0),当k=±1时,直线RT的方程为x=3,也过E(3,0),综上所述,直线RT恒过定点E(3,0).
解答 解:(Ⅰ)设动点M(x,y),A(x1,y1),B(x2,y2),设AB:x=my+n
$\left\{\begin{array}{l}{x=my+n}\\{{y}^{2}=4x}\end{array}\right.$,整理得:y2-4my-4n=0,
由韦达定理可知:y1•y2=-4n,则16x1•x2=(y1•y2)2=16n2,
∴x1•x2=n2,
由OA⊥OB,
即$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
∴y1y2+x1x2=0,
∴n2-4n=0即n①
而OM⊥AB,
∴$m=\frac{y}{x}$②
将①②代入x=my+n,整理得:x2+y2-4x=0(x≠0);
(Ⅱ)证明:设P、Q两点坐标分别为(x3,y4),(x4,y4),则点R的坐标为($\frac{{x}_{3}+{x}_{4}}{2}$,$\frac{{y}_{3}+{y}_{4}}{2}$)
显然直线斜率存在且不为0,由题意可设直线的方程为y=k(x-1)(k≠0),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,整理得:k2x2-(2k2+4)x+k2=0,
△=(2k2+4)2-4k4=16k2+16>0,
由韦达定理可知:x3+x4=2+$\frac{4}{{k}^{2}}$,则y3+y4=k(x3+x4-2)=$\frac{4}{k}$,
∴点R点坐标为(1+$\frac{2}{{k}^{2}}$,$\frac{2}{k}$),
由直线l2的斜率为-$\frac{1}{k}$,同理可得点T坐标为(1+2k2,-2k),
当k≠±1时,有$1+\frac{2}{k^2}≠1+2{k^2}$,此时直线RT的斜率${k_{RT}}=\frac{{\frac{2}{k}+2k}}{{1+\frac{2}{k^2}-1-2{k^2}}}=\frac{k}{{1-{k^2}}}$.
∴直线RT的方程为y+2k=$\frac{k}{1-{k}^{2}}$(x-1-2k2),
整理得:yk2+(x-3)k-y=0,
于是,直线RT恒过定点E(3,0);(10分)
当k=±1时,直线RT的方程为x=3,也过E(3,0).
综上所述,直线RT恒过定点E(3,0).(12分)
点评 本题考查直线与抛物线的位置关系,考查韦达定理,弦长公式及中点坐标公式的应用,考查直线方程的应用,考查计算能力,属于中档题.

| A. | 50 | B. | 100 | C. | 150 | D. | 200 |

| A. | -1 | B. | -$\frac{1}{8}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
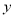 关于月份
关于月份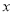 的线性回归方程;
的线性回归方程;
 ,
,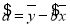 .
. 
 D,同时满足:
D,同时满足: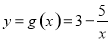 不存在“和谐区间”.
不存在“和谐区间”. (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值. 如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.
如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点. 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. 在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )


