题目内容
5.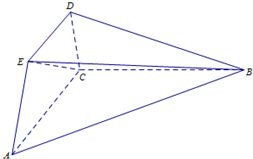 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.(Ⅰ)求证:平面ABE⊥平面BCE;
(Ⅱ)求二面角C-BE-D的正弦值.
分析 (Ⅰ)推导出AE⊥EC,从而BC⊥平面ACDE,进而BC⊥AE,AE⊥平面BCE,由此能证明平面ABE⊥平面BCE.
(Ⅱ)取AC的中点M,连结DM交EC于点F,过点F作FH⊥BE于点H,连结DH,则∠DHF为二面角C-BE-D的平面角,由此能求出二面角C-BE-D的正弦值.
解答 证明:(Ⅰ)如图1,∵AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2,
∴∠EAC=60°,∴AE⊥EC,
∵平面ABC⊥平面ACDE,交线为AC,∴BC⊥平面ACDE,
∴BC⊥AE,∴AE⊥平面BCE,
∵AE?平面ABE,∴平面ABE⊥平面BCE.
解:(Ⅱ)如图2,取AC的中点M,连结DM交EC于点F,
在等腰梯形ACDE中,由已知得DF∥AE,
由(Ⅰ)知AE⊥平面BCE,∴DF⊥平面BCE,
过点F作FH⊥BE于点H,连结DH,则DH⊥BE,
∴∠DHF为二面角C-BE-D的平面角,
∵DE=2,EB=$\sqrt{3+9+16}$=2$\sqrt{7}$,BD=$\sqrt{3+1+16}$=2$\sqrt{5}$,
又DE=2,∴由余弦定理得cos∠EBD=$\frac{28+20-4}{2×2\sqrt{7}×2\sqrt{5}}$=$\frac{11}{2\sqrt{35}}$,∴sin∠EBD=$\frac{\sqrt{19}}{2\sqrt{35}}$,
∴DH=DBsin$∠EBD=\frac{\sqrt{19}}{\sqrt{7}}$,
又在等腰△CDE中,由题意得DF=1,
∴在Rt△DFH中,sin$∠DHF=\frac{\sqrt{7}}{\sqrt{19}}$=$\frac{\sqrt{133}}{19}$,
∴二面角C-BE-D的正弦值为$\frac{\sqrt{133}}{19}$.
点评 本题考查面面垂直的证明,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的合理运用.

 的人数为( )
的人数为( )
 如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.
如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点. 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2. 在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为( )



 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.