题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c,若c2=(a-b)2+6,C=
,则△ABC的面积是( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
考点:余弦定理
专题:解三角形
分析:将“c2=(a-b)2+6”展开,另一方面,由余弦定理得到c2=a2+b2-2abcosC,比较两式,得到ab的值,计算其面积.
解答:
解:由题意得,c2=a2+b2-2ab+6,
又由余弦定理可知,c2=a2+b2-2abcosC=a2+b2-ab,
∴-2ab+6=-ab,即ab=6.
∴S△ABC=
absinC=
.
故选:C.
又由余弦定理可知,c2=a2+b2-2abcosC=a2+b2-ab,
∴-2ab+6=-ab,即ab=6.
∴S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
故选:C.
点评:本题是余弦定理的考查,在高中范围内,正弦定理和余弦定理是应用最为广泛,也是最方便的定理之一,高考中对这部分知识的考查一般不会太难,有时也会和三角函数,向量,不等式等放在一起综合考查.

练习册系列答案
相关题目
已知复数z满足(3-4i)z=25,则z=( )
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
i是虚数单位,复数
=( )
| 7+i |
| 3+4i |
| A、1-i | ||||
| B、-1+i | ||||
C、
| ||||
D、-
|
已知函数f(x)=5|x|,g(x)=ax2-x(a∈R),若f[g(1)]=1,则a=( )
| A、1 | B、2 | C、3 | D、-1 |
某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
| A、0.8 | B、0.75 |
| C、0.6 | D、0.45 |
对任意x,y∈R,|x-1|+|x|+|y-1|+|y+1|的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
 幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图),设点A(1,0)、B(0,1),若y=xα,y=xβ的图象与线段AB分别交于M、N,且
幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图象是一族美丽的曲线(如图),设点A(1,0)、B(0,1),若y=xα,y=xβ的图象与线段AB分别交于M、N,且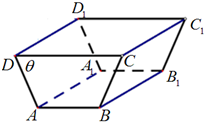 某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<
某农户准备建一个水平放置的直四棱柱形储水窖(如图),其中直四棱柱的高AA1=10m,两底面ABCD,A1B1C1D1是高为2m,面积为10m2的等腰梯形,且∠ADC=θ(0<θ<