题目内容
17.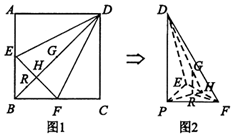 如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.(I)若λ=2,求证:GR⊥平面PEF;
(Ⅱ)是否存在正实数λ,使得直线FR与平面DEF所成角的正弦值为$\frac{{2\sqrt{2}}}{5}$?若存在,求出λ的值;若不存在,请说明理由.
分析 (I)若λ=2,证明PD⊥平面PEF,GR∥PD,即可证明:GR⊥平面PEF;
(Ⅱ)建立如图所示的坐标系,求出平面DEF的一个法向量,利用直线FR与平面DEF所成角的正弦值为$\frac{{2\sqrt{2}}}{5}$,建立方程,即可得出结论.
解答 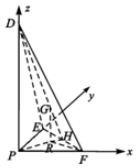 (I)证明:由题意,PE,PF,PD三条直线两两垂直,∴PD⊥平面PEF,
(I)证明:由题意,PE,PF,PD三条直线两两垂直,∴PD⊥平面PEF,
图1中,EF∥AC,∴GB=2GH,
∵G为BD中点,∴DG=2GH.
图2中,∵$\frac{PR}{GH}=\frac{BR}{RH}$=2,∴△PDH中,GR∥PD,
∴GR⊥平面PEF;
(Ⅱ)解:由题意,建立如图所示的坐标系,设PD=4,则P(0,0,0),F(2,0,0),E(0,2,0),D(0,0,4),∴H(1,1,0),
∵$\frac{PR}{RH}$=λ,∴R($\frac{λ}{1+λ}$,$\frac{λ}{1+λ}$,0),
∴$\overrightarrow{RF}$=($\frac{2+λ}{1+λ}$,-$\frac{λ}{1+λ}$,0),
∵$\overrightarrow{EF}$=(2,-2,0),$\overrightarrow{DE}$=(0,2,-4),
设平面DEF的一个法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{2x-2y=0}\\{2y-4z=0}\end{array}\right.$,取$\overrightarrow{m}$=(2,2,1),
∵直线FR与平面DEF所成角的正弦值为$\frac{{2\sqrt{2}}}{5}$,
∴$\frac{\frac{4}{1+λ}}{3\sqrt{(\frac{2+λ}{1+λ})^{2}+(-\frac{λ}{1+λ})^{2}}}$=$\frac{2\sqrt{2}}{5}$,
∴λ=$\frac{1}{3}$,
∴存在正实数λ=$\frac{1}{3}$,使得直线FR与平面DEF所成角的正弦值为$\frac{{2\sqrt{2}}}{5}$.
点评 本题考查了线面垂直的判定,线面角的计算,考查向量方法的运用,属于中档题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.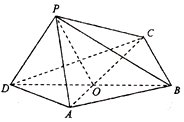 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,BD=2$\sqrt{3}$,AC与BD交于O点.将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为θ,且P点在平面ABCD内的射影落在△ACD内.