题目内容
7.若满足条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≤0}\\{y≥a}\end{array}\right.$的整点(x,y)恰有9个,其中整点是指横、纵坐标都是整数的点,则整数a的值为-1.分析 作出满足条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≤0}\\{y≥a}\end{array}\right.$的平面区域,利用整点(x,y)恰有9个,可求整数a的值.
解答  解:作出满足条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≤0}\\{y≥a}\end{array}\right.$的平面区域,如图:
解:作出满足条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-2≤0}\\{y≥a}\end{array}\right.$的平面区域,如图:
要使整点(x,y)恰有9个,即为(0,0)、(1,0)、(2,0),(1,1)、(-1,-1)、(0,-1)、(1,-1),(2,-1)、(3,-1)
故整数a的值为-1
故答案为:-1.
点评 本题考查线性规划知识,考查整点的含义,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
18.设集合A={x|-1<x<2},B={x|y=lg(x-1)},则A∩(∁RB)=( )
| A. | (-1,1) | B. | [2,+∞) | C. | (-1,1] | D. | [-1,+∞) |
19.目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
| 善于使用学案 | 不善于使用学案 | 总计 | |
| 学习成绩优秀 | 40 | ||
| 学习成绩一般 | 30 | ||
| 总计 | 100 |
参考数据:
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.
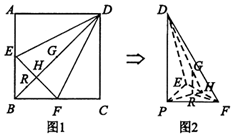 如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.
如图1,在正方形ABCD中,点E,F分别是AB,BC的中点,BD与EF交于点H,G为BD中点,点R在线段BH上,且$\frac{BR}{RH}$=λ(λ>0).现将△AED,△CFD,△DEF分别沿DE,DF,EF折起,使点A,C重合于点B(该点记为P),如图2所示.