题目内容
19.设函数f(x)=(a-2)1n(-x)+$\frac{1}{x}$+2ax(a∈R).(1)当a=0时,求f(x)的极值;
(2)当a<0时,求f(x)的单调区间.
分析 (1)求出f(x)的对数,解关于导函数的不等式,得到函数的单调区间,从而求出函数的极值即可;
(2)求出函数的导数,得到导函数小于0,从而求出函数递减.
解答 解:(1)f(x)的定义域是(-∞,0),
a=0时,f(x)=-2ln(-x)+$\frac{1}{x}$,x<0,
f′(x)=-$\frac{2}{x}$-$\frac{1}{{x}^{2}}$=$\frac{-2x-1}{{x}^{2}}$,
令f′(x)>0,解得:x<-$\frac{1}{2}$,令f′(x)<0,解得:-$\frac{1}{2}$<x<0,
∴f(x)在(-∞,-$\frac{1}{2}$)递增,在(-$\frac{1}{2}$,0)递减,
∴f(x)最大值=f(-$\frac{1}{2}$)=2ln2-2;
(2)a<0时,f′(x)=$\frac{(ax+1)(2x-1)}{{x}^{2}}$,
∵x<0,a<0,∴ax+1>0,2x-1<0,
∴f′(x)<0在(-∞,0)恒成立,
∴f(x)在(-∞,0)递减.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
11.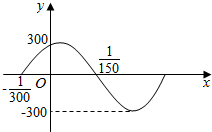 如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )
如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )
 如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )
如图,表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin(ωt+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象,则该函数解析式是( )| A. | y=300sin(50πt+$\frac{π}{3}$) | B. | y=300sin(50πt-$\frac{π}{3}$) | ||
| C. | y=300sin(100πt+$\frac{π}{3}$) | D. | y=300sin(100πt-$\frac{π}{3}$) |