题目内容
△ABC中,sinB既是sinA,sinC的等差中项,又是sinA,sinC的等比中项,则∠B= .
考点:等比数列的性质,等差数列的性质
专题:等差数列与等比数列
分析:由题设知
,由此推导出sinB=sinA=sinC,从而能求出∠B=
.
|
| π |
| 3 |
解答:
解:∵△ABC中,sinB既是sinA,sinC的等差中项,
又是sinA,sinC的等比中项,
∴
,
∴4sin2B=(sinA+sinC)2
即:4sinA•sinC=(sinA+sinC)2
(sinA+sinC)2-4sinA•sinC=0
(sinA-sinC)2=0
∴sinA=sinC
∴2sinB=2sinA=2sinC
∴sinB=sinA=sinC
∴a=b=c
∴∠B=
.
故答案为:
.
又是sinA,sinC的等比中项,
∴
|
∴4sin2B=(sinA+sinC)2
即:4sinA•sinC=(sinA+sinC)2
(sinA+sinC)2-4sinA•sinC=0
(sinA-sinC)2=0
∴sinA=sinC
∴2sinB=2sinA=2sinC
∴sinB=sinA=sinC
∴a=b=c
∴∠B=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查角的求法,是中档题,解题时要熟练掌握等差数列、等比数列的性质的灵活运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
如图给出一个算法的程序框图,该程序框图的功能是( )
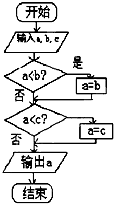

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
若x、y满足不等式
,则z=3x+y的最大值为( )
|
| A、11 | B、-11 |
| C、13 | D、-13 |
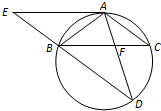 如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.