题目内容
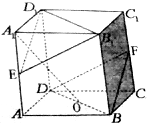已知正方体ABCD-A1B1C1D1中，E、F分别是AA1、CC1的中点，则（1）异面直线D1C1与BD所成的角的大小是
（2）求证：BD∥平面B1D1E；
（3）求证：平面BDF∥平面B1D1E．
考点：平面与平面平行的判定,异面直线及其所成的角,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由条件利用正方体的性质，可得异面直线D1C1与BD所成的角即∠BDC，从而得到答案．
（2）由正方体的性质可得BD∥B1D1，再利用直线和平面平行的判定定理证得 BD∥平面B1D1E．
（3）证明BF∥D1E，利用直线和平面平行的判定定理证得BF∥平面B1D1E．结合（2）的结论以及BF∩BD=B，利用平面和平面平行判定定理证得平面BDF∥平面B1D1E．
（2）由正方体的性质可得BD∥B1D1，再利用直线和平面平行的判定定理证得 BD∥平面B1D1E．
（3）证明BF∥D1E，利用直线和平面平行的判定定理证得BF∥平面B1D1E．结合（2）的结论以及BF∩BD=B，利用平面和平面平行判定定理证得平面BDF∥平面B1D1E．
解答：
解：（1）正方体ABCD-A1B1C1D1中，由于D1C1∥DC，故异面直线D1C1与BD所成的角即∠BDC，
而∠BDC=45°，∴异面直线D1C1与BD所成的角的大小是45°，
故答案为：45°．
（2）由正方体的性质可得BD∥B1D1，而B1D1?平面B1D1E，BD不在平面B1D1E内，
∴BD∥平面B1D1E．
（3）取DD1的中点M，则D1E∥MA，而MA∥BF，∴BF∥D1E．
而D1E?平面B1D1E，BF不在平面B1D1E中，故有BF∥平面B1D1E．
再由BD∥平面B1D1E，且BF∩BD=B，∴平面BDF∥平面B1D1E．
而∠BDC=45°，∴异面直线D1C1与BD所成的角的大小是45°，
故答案为：45°．
（2）由正方体的性质可得BD∥B1D1，而B1D1?平面B1D1E，BD不在平面B1D1E内，
∴BD∥平面B1D1E．
（3）取DD1的中点M，则D1E∥MA，而MA∥BF，∴BF∥D1E．
而D1E?平面B1D1E，BF不在平面B1D1E中，故有BF∥平面B1D1E．
再由BD∥平面B1D1E，且BF∩BD=B，∴平面BDF∥平面B1D1E．
点评：本题主要考查求异面直线所成的角，直线和平面平行的判定定理、平面和平面平行判定定理的应用，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
+1，则对任意实数x1、x2，且0＜x1＜x2＜2，都有（ ）
| 2x-x2 |
| A、x1f（x2）＜x2f（x1） |
| B、x1f（x2）＞x2f（x1） |
| C、x1f（x1）＜x2f（x2） |
| D、x1f（x1）＞x2f（x2） |