题目内容
已知两个动点P,Q分别在两条直线l1:y=x和l2:y=-x上运动,且它们的横坐标分别为角θ的正弦,余弦,θ∈[0,π].记
=
+
,求动点M的轨迹的普通方程.
| OM |
| OP |
| OQ |
考点:轨迹方程
专题:计算题,直线与圆
分析:设M(x,y),根据
=
+
,可得
两式平方相加得动点M的轨迹的普通方程.
| OM |
| OP |
| OQ |
|
解答:
解:设M(x,y),则
…(2分)
两式平方相加得x2+y2=2. …(5分)
又x=
sin(θ+
),y=
sin(θ-
),θ∈[0,π],
所以x∈[-1,
],y∈[-1,
].…(8分)
所以动点M轨迹的普通方程为x2+y2=2(x,y∈[-1,
]).…(10分)
|
两式平方相加得x2+y2=2. …(5分)
又x=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
所以x∈[-1,
| 2 |
| 2 |
所以动点M轨迹的普通方程为x2+y2=2(x,y∈[-1,
| 2 |
点评:本题考查了轨迹方程的求法,考查了数学转化思想方法,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设M={0,1,2,4,5,8},N={0,2,3,5},则N∩M=( )
| A、{1,3} |
| B、{1,4,8} |
| C、{0,2,5} |
| D、{2,4,6} |
设双曲线C1,抛物线C2的焦点均在x轴上,C1的中心与C2的顶点均为原点,从每条曲线上至少取一个点,将其坐标记录如下:
则在C1和C2上点的个数分别是( )
| x | 1 |
|
| 2 | 3 | ||||||
| y | 2
|
| 2 | 4 | 2
|
| A、1,4 | B、2,3 |
| C、4,1 | D、3,3 |
下列各点中,不在方程x2-xy+2y+1=0表示的曲线上的点是( )
| A、(1,-2) |
| B、(-2,1) |
| C、(-3,-2) |
| D、(3,10) |
若实数x,y满足
,若z=x+2y,则z的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
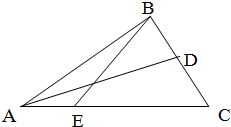 如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若
如图,在△ABC中,D是BC的中点,E是AC的三等分点,且EC=2AE,若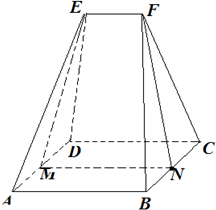 如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
如图,五面体ABCDEF中,底面ABCD为矩形,AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6