题目内容
如图,已知正方形ABCD和矩形AC EF所在的平面互相垂直,AB=
EF所在的平面互相垂直,AB=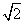 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证:AM∥平面BDE;
(2)试在线段AC上确定一点P,使得PF与CD所成的角是60°.

解:

(1)证明:如图建立空间直角坐标系.设AC∩BD=N,连接NE,
则N( ,
, ,0),E(
,0),E( 0,0,1),
0,0,1),
∴ =(-
=(- ,-
,- ,1).
,1).
又A(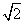 ,
,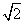 ,0),M(
,0),M( ,
, ,1),
,1),
∴ =(-
=(- ,-
,- ,1),
,1),
∴ =
= 且NE与AM不共线.∴NE∥AM.
且NE与AM不共线.∴NE∥AM.
又NE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE.
(2)设P(t,t,0)(0≤t≤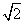 ),
),
则 =(
=(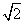 -t,
-t,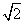 -t,1),
-t,1), =(
=(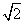 ,0,0).
,0,0).
又∵ 与
与 所成的角为60°,
所成的角为60°,
则
解之,得t= 或t=
或t= (舍去),故点P为AC的中点.
(舍去),故点P为AC的中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 CD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为( )
CD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为( ) B.
B.
 a3 D.
a3 D. a3
a3
 D.2
D.2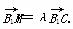 若向量
若向量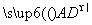 与
与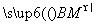 的夹角小于45°,求实数λ的取值范围.
的夹角小于45°,求实数λ的取值范围.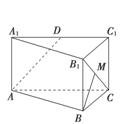
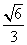 B.
B.
 D.
D.
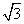
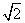 D.1
D.1 .
.