题目内容
已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:(1)过定点A(-3,4);(2)斜率为 .
.
解:(1)设直线l的方程是y=k(x+3)+4,
它在x轴、y轴上的截距分别是- -3,3k+4,
-3,3k+4,
由已知,得|(3k+4)(- -3)|=6,
-3)|=6,
解得k1=- 或k2=-
或k2=- .
.
所以直线l的方程为2x+3y-6=0或8x+3y+12=0.
(2)设直线l在y轴上的截距为b,
则直线l的方程是y= x+b,它在x轴上的截距是-6b,
x+b,它在x轴上的截距是-6b,
由已知,得|-6b·b|=6,∴b=±1.
∴直线l的方程为x-6y+6=0或x-6y-6=0.

练习册系列答案
相关题目
某市居民2008~2012年家庭年平均收入x(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
| 收入x | 11.5 |
| 13 | 13.3 |
|
| 支出Y | 6.8 | 8.8 | 9.8 | 10 | 12 |
根据统计资料,居民家庭年平均收入的中位数是 ,家庭年平均收入与年平均支出有__________线性相关关系.(第二个空填“正”或“负”)
 EF所在的平面互相垂直,AB=
EF所在的平面互相垂直,AB=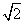 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
 12.1
12.1 15
15 B.2
B.2 D.0
D.0 点按逆时针方向旋转45°得到直线m,若直线l和m分别和y轴交于Q、R两点.
点按逆时针方向旋转45°得到直线m,若直线l和m分别和y轴交于Q、R两点. 若l1∥l2,则θ=________.
若l1∥l2,则θ=________.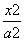 +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) B.
B.
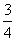 D.
D.