题目内容
4.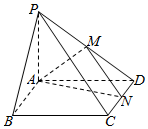 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点(Ⅰ)判断直线MN与平面PAC的位置关系,并给予证明
(Ⅱ)求三棱锥P-AMN的体积.
分析 (I)由中位线定理可得MN∥PC,故而MN∥平面PAC;
(II)用三棱锥P-ADN的体积减去三棱锥M-ADN的体积即可.
解答 解:(I)MN∥平面PAC.
证明:∵M,N是PD,PC的中点,
∴MN∥PC,
∵PC?平面PAC,MN?平面PAC,
∴MN∥平面PAC.
(II)S△ADN=$\frac{1}{2}AD×DN$=$\frac{1}{2}×2×1=1$,
V棱锥P-ADN=$\frac{1}{3}{•S}_{△ADN}•PA$=$\frac{2}{3}$,
V棱锥M-ADN=$\frac{1}{3}•{S}_{△ADN}•\frac{1}{2}PA$=$\frac{1}{3}$.
∴V棱锥P-AMN=V棱锥P-ADN-V棱锥M-ADN=$\frac{1}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
19.“x<4”是“|x-2|<1”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.已知集合M={x|-1<x<2},集合N={x|x(x+2)<0},则M∪N=( )
| A. | (-2,2) | B. | (-1,0) | C. | R | D. | ∅ |
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
14.函数f(x)=Asin(ωx+$\frac{ωπ}{2}$)(A>0,ω>0)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,则ω的最大值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{11}$ |