题目内容
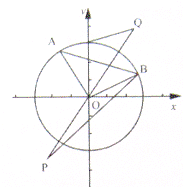如图：点A，B是单位圆圆O上不同的两点，设| OA |
| a |
| OB |
| b |
（1）求证：（
| a |
| b |
| a |
| b |
（2）线段PQ以点O为中点，且|PQ|=2|AB|，若两个向量k
| a |
| b |
| a |
| b |
| BP |
| AQ |
| BP |
| AQ |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）
=a，
=
，且|
|=|
|=1，由此能证明（
+
）⊥（
-
）．
（2）由题意知(k
+
)2=(
-k
)2，OA⊥OB，由此推导出
•
=(
-
)•(
-
)=-2-2cosθ，从而得到当θ=π时，
•
取得最大值为0．
| OA |
| OB |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）由题意知(k
| a |
| b |
| a |
| b |
| BP |
| AQ |
| OP |
| OB |
| OQ |
| OA |
| BP |
| AQ |
解答：
（1）证明：∵点A，B是单位圆上不同的两点，
∴
=a，
=
，
∴|
|=|
|=1，
又∵(
+
)•(
-
)=
2-
2=0，
∴（
+
）⊥（
-
）．
（2）解：∵两个向量k
+
与
-k
的模相等，k≠0，k∈R，
∴(k
+
)2=(
-k
)2，
即k2
2+2k
•
+
2=
2-2k
•
+k2
2，
∵|
|=|
|=1，k≠0，k∈R，
∴
•
=0，∴OA⊥OB，
∴
•
=0，|PQ|=2|AB|=
，
∴线段PQ以点O为中点，即|
|=|
|=
，
又
=
-
，
=
-
，
=-
，
∴
•
=(
-
)•(
-
)
=
•
-
•
-
•
+
•
=-2-
•
-
•
=-2+
•
-
•
=-2+
(
-
)
=-2+
•
=-2-
•
=-2-2cosθ，
∴当θ=π时，
•
取得最大值为0．
∴
| OA |
| OB |
| b |
∴|
| a |
| b |
又∵(
| a |
| b |
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| b |
（2）解：∵两个向量k
| a |
| b |
| a |
| b |
∴(k
| a |
| b |
| a |
| b |
即k2
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
∵|
| a |
| b |
∴
| a |
| b |
∴
| OB |
| OA |
| 2 |
∴线段PQ以点O为中点，即|
| OP |
| OQ |
| 2 |
又
| BP |
| OP |
| OB |
| AQ |
| OQ |
| OA |
| OP |
| OQ |
∴
| BP |
| AQ |
| OP |
| OB |
| OQ |
| OA |
=
| OP |
| OQ |
| OP |
| OA |
| OB |
| OQ |
| OB |
| OA |
=-2-
| OP |
| OA |
| OB |
| OQ |
=-2+
| OQ |
| OA |
| OB |
| OQ |
=-2+
| OQ |
| OA |
| OB |
=-2+
| OQ |
| BA |
=-2-
| OQ |
| AB |
=-2-2cosθ，
∴当θ=π时，
| BP |
| AQ |
点评：本题考查向量垂直的证明，考查向量的数量积的最大值的求法，解题时要认真审题，注意单位圆的性质的灵活运用．
练习册系列答案
相关题目
