题目内容
已知在等比数列{an}中,a4=27,q=-
,则a6= ,通项公式an= .
| 1 |
| 3 |
考点:等比数列的通项公式,等比数列的性质
专题:等差数列与等比数列
分析:利用等比数列的通项公式求解.
解答:
解:∵在等比数列{an}中,a4=27,q=-
,
∴a6=a4q2=27×(-
)2=3.
a1=
=
=-729.
∴an=(-729)•(-
)n-1.
故答案为:3,(-729)•(-
)n-1.
| 1 |
| 3 |
∴a6=a4q2=27×(-
| 1 |
| 3 |
a1=
| a4 |
| q3 |
| 27 | ||
(-
|
∴an=(-729)•(-
| 1 |
| 3 |
故答案为:3,(-729)•(-
| 1 |
| 3 |
点评:本题考查等比数列的通项公式的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
若函数f(x)=loga(2x2+x)(a>0,a≠1)在区间(
,1)内恒有f(x)>0,则f(x)的单调递增区间是( )
| 1 |
| 2 |
A、(-∞,-
| ||
B、(-
| ||
C、(-∞,-
| ||
| D、(0,+∞) |
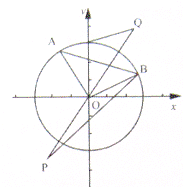 如图:点A,B是单位圆圆O上不同的两点,设
如图:点A,B是单位圆圆O上不同的两点,设