题目内容
12.已知棱长为1的正方体ABCD-A1B1C1D1中,$\overrightarrow{AE}$=λ$\overrightarrow{AB}$,$\overrightarrow{{D_1}F}$=μ$\overrightarrow{{D_1}B}$,其中λ∈(0,1),μ∈(0,1),满足EF∥平面AA1D1D,则当三棱锥A-EFB1的体积最大时,λ+μ的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
分析 连结AD1,则由线面平行的性质得EF∥AD1,于是$EF=\sqrt{2}(1-λ)$,AE=λ=μ.过A1作A1M⊥AD1,则A1M⊥平面ABD1,AB⊥EF.A1M=$\frac{A{A}_{1}•{A}_{1}{D}_{1}}{A{D}_{1}}$=$\frac{\sqrt{2}}{2}$.所以V${\;}_{A-EF{B}_{1}}$=V${\;}_{{B}_{1}-AEF}$=V${\;}_{{A}_{1}-AEF}$$\frac{1}{3}{S}_{△AEF}•{A}_{1}M$,使用基本不等式求出体积取得最大值时成立的条件,从而得到λ,μ的值.
解答 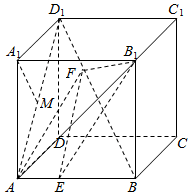 解:连结AD1,∵EF∥平面AA1D1D,EF?平面ABD1,平面ABD1∩平面AA1D1D=AD1
解:连结AD1,∵EF∥平面AA1D1D,EF?平面ABD1,平面ABD1∩平面AA1D1D=AD1
∴EF∥AD1,∴$\frac{EF}{A{D}_{1}}=\frac{BE}{AB}=1-λ$,∴$EF=\sqrt{2}(1-λ)$,AE=λ=μ.
过A1作A1M⊥AD1,
∵AB⊥平面AA1D1D,A1M?平面AA1D1D,AD1?平面AA1D1D,
∴AB⊥AD1,AB⊥A1M,
∴A1M⊥平面ABD1,AB⊥EF.
∵A1M=$\frac{A{A}_{1}•{A}_{1}{D}_{1}}{A{D}_{1}}$=$\frac{\sqrt{2}}{2}$.
∴V${\;}_{A-EF{B}_{1}}$=V${\;}_{{B}_{1}-AEF}$=V${\;}_{{A}_{1}-AEF}$=$\frac{1}{3}{S}_{△AEF}•{A}_{1}M$=$\frac{1}{3}×\frac{1}{2}×λ×\sqrt{2}(1-λ)×\frac{\sqrt{2}}{2}$=$\frac{1}{6}$λ(1-λ)≤$\frac{1}{6}×(\frac{λ+1-λ}{2})^{2}$=$\frac{1}{24}$.
当且仅当λ=1-λ即$λ=\frac{1}{2}$时取等号,∴λ+μ=1.
故选D
点评 本题考查了正方体的结构特征,线面平行的性质,棱锥的体积计算,属于中档题.

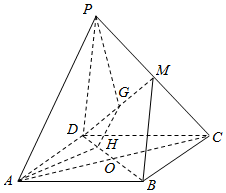 如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.