题目内容
方程lg(x+1)+1=lg(x2-1)的解是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:方程即即 lg10(x+1)=lg(x+1)(x-1),可得x2-1=10(x+1)>0 ②.分别解①、②求得x的值,可得结论.
解答:
解:方程lg(x+1)+1=lg(x2-1),即 lg10(x+1)=lg(x2-1),
∴x2-1=10(x+1)>0,求得x=11,
故答案为:x=11.
∴x2-1=10(x+1)>0,求得x=11,
故答案为:x=11.
点评:本题主要考查对数方程的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
下列函数中,在(0,+∞)上为增函数的是( )
A、y=(
| ||
B、y=log
| ||
C、y=
| ||
| D、y=x3 |
双曲线x2-y2=2的顶点到其渐进线的距离等于( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
 如图,平面α与平面β交于直线l,A,C是平面α内不同的两点,B,D是平面β内不同的两点,且A,B,C,D不在直线l上,M,N分别是线段AB,CD的中点,下列判断错误的是
如图,平面α与平面β交于直线l,A,C是平面α内不同的两点,B,D是平面β内不同的两点,且A,B,C,D不在直线l上,M,N分别是线段AB,CD的中点,下列判断错误的是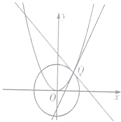 如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=
如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p= 如图是一个边长为1的正方形,M为所在边上的中点,若随机掷一粒绿豆,则这粒绿豆落到阴影部分的概率为
如图是一个边长为1的正方形,M为所在边上的中点,若随机掷一粒绿豆,则这粒绿豆落到阴影部分的概率为