设全集为R.集合A={x∈Z|-1＜x≤3}.集合B={1.2}.则集合A∩(∁RB)=( )A．{0.3}B．{-1.0.1.2.3}C．{-1.0.3}D．{-1.0} 题目和参考答案——青夏教育精英家教网—

题目内容

5．设全集为R，集合A={x∈Z|-1＜x≤3}，集合B={1，2}，则集合A∩（∁_RB）=（　　）

A．

{0，3}

B．

{-1，0，1，2，3}

C．

{-1，0，3}

D．

{-1，0}

分析根据补集与交集的定义，写出∁_RB与A∩（∁_RB）即可．

解答解：全集为R，集合A={x∈Z|-1＜x≤3}={0，1，2，3}，
集合B={1，2}，∴∁_RB={x∈R|x≠1且x≠2}，
∴集合A∩（∁_RB）={0，3}．
故选：A．

点评本题考查了交集与补集的定义与运算问题，是基础题目．

练习册系列答案

16．已知函数f_n（x）（n∈N^*）具有下列性质：f_n（0）=$\frac{1}{2}$；n[f_n（$\frac{k+1}{n}$）-f_n（$\frac{k}{n}$）]=[f_n（$\frac{k}{n}$）-1]f_n（$\frac{k+1}{n}$））（k=0，1，2，…，n-1）．
（1）当n一定时，记a_k=$\frac{1}{{f}_{n}（\frac{k}{n}）}$，求a_k的表达式（k=0，1，2，…，n-1）；
（2）对n∈N^*，证明$\frac{1}{4}$＜f_n（1）$≤\frac{1}{3}$．

13．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线与直线x=$\frac{{a}^{2}}{c}$交于点M，设其右焦点为F，且点F到渐近线的距离为d，则（　　）

20．对于满足|f（n+1）-f（n）|≤（$\frac{1}{10}$）ⁿ（n∈N）的所有f（n），若f（0）=1，则f（10）的值所在的区间一定是（　　）

（-$\frac{1}{9}$，$\frac{19}{9}$）

D．

（-$\frac{1}{5}$，$\frac{9}{5}$）

10．

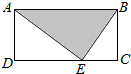在长方形ABCD中，AB=3，BC=2，E为CD上一点，将一个质点随机投入长方形中，则质点落在阴影部分的概率为$\frac{1}{2}$．

17．已知函数f（x）=mlnx-x²+2（m∈R）．
（Ⅰ）当m=1时，求f（x）的单调区间；
（Ⅱ）若f（x）在x=1时取得极大值，求证：f（x）-f′（x）≤4x-3；
（Ⅲ）若m≤8，当x≥1时，恒有f（x）-f′（x）≤4x-3恒成立，求m的取值范围．

14．一位网民在网上光顾某网店，经过一番浏览后，对该店铺中的A，B，C三种商品有购买意向．已知该网民购买A种商品的概率为$\frac{3}{4}$，购买B种商品的槪率为$\frac{2}{3}$，购买C种商品的概率为$\frac{1}{2}$．假设该网民是否购买这三种商品相互独立
（1）求该网民至少购买2种商品的概率；
（2）用随机变量η表示该网民购买商品的种数，求η的槪率分布和数学期望．

15．设f（x）=log${\;}_{\frac{1}{2}}$x-a^x＞0在（0，$\frac{1}{4}$）上恒成立，a＞0且a≠1，求a范围（　　）

试题分类