题目内容
设定义在R上的函数f(x)是最小正周期为2π的偶函数,当x∈[0,π]时,f(x)=sin2x,则函数y=f(x)-cosx在[-π,2π]上的零点个数为( )
| A、6 | B、7 | C、8 | D、9 |
考点:函数零点的判定定理
专题:函数的性质及应用,三角函数的图像与性质
分析:根据已知在同一坐标系中画出函数y=f(x)和y=cosx在[-π,2π]上的图象,分析函数y=f(x)和y=cosx在[-π,2π]上的图象交点的个数,可得答案.
解答:
解:∵函数f(x)是最小正周期为2π的偶函数,当x∈[0,π]时,f(x)=sin2x,
∴函数y=f(x)和y=cosx在[-π,2π]上的图象如下图所示:
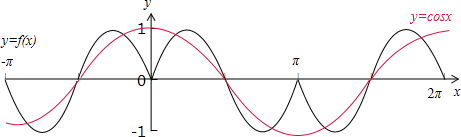
由图可知函数y=f(x)和y=cosx在[-π,2π]上的图象共有9个交点,
故函数y=f(x)-cosx在[-π,2π]上有9个零点,
故选:D
∴函数y=f(x)和y=cosx在[-π,2π]上的图象如下图所示:

由图可知函数y=f(x)和y=cosx在[-π,2π]上的图象共有9个交点,
故函数y=f(x)-cosx在[-π,2π]上有9个零点,
故选:D
点评:本题考查的知识点是函数零点的求法,根据已知画出函数y=f(x)和y=cosx在[-π,2π]上的图象,将函数零点问题转化为图象交点问题,是解答的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
设函数f(x)在R 上有定义,给出下列函数:
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知角α的终边经过点P(3t,-4t)(t≠0),则sinα+cosα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、±
|
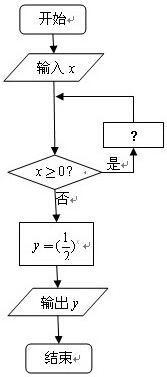 执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )
执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )①x=x-1②x=x-2③x=x-3④x=x-4.
| A、①②③ | B、②③ |
| C、②③④ | D、③④ |
下列式子中,表示残差平方和的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知椭圆的中心在原点,长轴长为6,一条准线方程为x=9,则该椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线l:y+kx+2=0与曲线C:ρ=2cosθ有交点,则k的取值范围是( )
A、k≤-
| ||
B、k≥-
| ||
| C、k∈R | ||
| D、k∈R但k≠0 |
结论为:xn+yn能被x+y整除,令n=1,2,3,4验证结论是否正确,得到此结论成立的条件可以为( )
| A、n∈N* |
| B、n∈N*且n≥3 |
| C、n为正奇数 |
| D、n为正偶数 |

