题目内容
4.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{x+y≥0}\\{x+2y-4≥0}\end{array}\right.$,则z=x-2y的最大值为$-\frac{1}{2}$.分析 由题意作平面区域,化简z=3x-2y为y=$\frac{1}{2}$x-$\frac{1}{2}z$,从而可得-$\frac{1}{2}z$是直线y=$\frac{1}{2}$x-$\frac{1}{2}z$的截距,从而解得.
解答 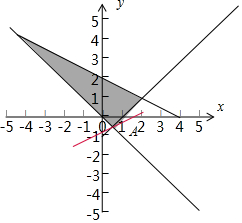 解:由题意作变量x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{x+y≥0}\\{x+2y-4≥0}\end{array}\right.$平面区域如图,
解:由题意作变量x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{x+y≥0}\\{x+2y-4≥0}\end{array}\right.$平面区域如图,
化简z=x-2y为y=$\frac{1}{2}$x-$\frac{1}{2}z$,-$\frac{z}{2}$是直线y=$\frac{1}{2}$x-$\frac{1}{2}z$的截距,
由$\left\{\begin{array}{l}{x+y=0}\\{x-y-1=0}\end{array}\right.$,解得A($\frac{1}{2}$,-$\frac{1}{2}$)
故过点A($\frac{1}{2},-\frac{1}{2}$)时,
z=x-2y有最大值为$\frac{1}{2}$-2×$\frac{1}{2}$=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题考查了线性规划的解法及数形结合的思想应用.

练习册系列答案
相关题目
20.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,第二象限的点M在双曲线C的渐近线上,且|OM|=a,若直线MF的斜率为$\frac{b}{a}$,则双曲线C的渐近线方程为( )
| A. | y=±x | B. | y=±2x | C. | y=±3x | D. | y=±4x |
1.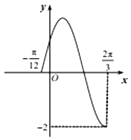 已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )
已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )
 已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )
已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
18.已知集合P={x|x-1≤0},M={x|x+2>0},则P∩M=( )
| A. | (-∞,1] | B. | [-2,+∞) | C. | [1,2) | D. | (-2,1] |
13.已知向量$\vec a$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,则向量$\overrightarrow{a}$与向量$\overrightarrow{a}$+2$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |