题目内容
3.在正方形ABCD中,AB=AD=2,M,N分别是边BC,CD上的动点,当|$\overrightarrow{AM}$|•|$\overrightarrow{AN}$|=4时,则|$\overrightarrow{MN}$|的取值范围是$[\sqrt{2},2]$.分析 由题意画出图形,由$\overrightarrow{AM}•\overrightarrow{AN}$=4,得x+y=2.再由|$\overrightarrow{MN}$|=$\sqrt{(x-2)^{2}+(y-2)^{2}}$的几何意义,即线段x+y=2(0≤x≤2,0≤y≤2)上的动点到定点(2,2)的距离求解.
解答 解:如图,以A为原点建立平面直角坐标系,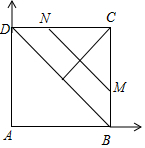
设M(2,y),N(x,2)(0≤x≤2,0≤y≤2),
则$\overrightarrow{AM}•\overrightarrow{AN}$=2x+2y=4,即x+y=2.
∴|$\overrightarrow{MN}$|=$\sqrt{(x-2)^{2}+(y-2)^{2}}$.
可以看做线段x+y=2(0≤x≤2,0≤y≤2)上的动点到定点(2,2)的距离.
最小值为$\sqrt{2}$,最大值为2.
故答案为:$[\sqrt{2},2]$.
点评 本题考查了数量积运算性质,考查数形结合的解题思想方法与数学转化思想方法,属于中档题.

练习册系列答案
相关题目
13.设变量x,y满足线性约束条件$\left\{\begin{array}{l}{x+y≤1}\\{x-y≤1}\\{x≥0}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
14.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x>1}\\{1-{x}^{3},x≤1}\end{array}\right.$,若函数y=f(x)-a(x-1)恰有三个零点,则实数a的取值范围是( )
| A. | (-$\frac{3}{4}$,0) | B. | (-∞,-$\frac{3}{4}$) | C. | (-3,-$\frac{3}{4}$) | D. | (0,1) |
18.在等差数列{an}中,Sn为其前n项和,若a3+a4+a8=25,则S9=( )
| A. | 60 | B. | 75 | C. | 90 | D. | 105 |
8.已知向量$\overrightarrow{BA}=(1,-3)$,向量$\overrightarrow{BC}=(4,-2)$,则△ABC的形状为( )
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |
15.中石化集团获得了某地深海油田块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点米布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见下表:
(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(Ⅱ)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的$\widehat{b}$,$\widehat{a}$的值($\widehat{b}$,$\widehat{a}$精确到0.01)与(I)中b,a的值差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井?(参考公式和计算结果:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\sum_{i=1}^{4}{{x}_{2i-1}}^{2}$=94,$\sum_{i=1}^{4}{x}_{2i-1}{y}_{2i-1}$=945)
(Ⅲ)设出油量与勘探深度的比值k不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数X的分布列与数学期望.
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(Ⅱ)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的$\widehat{b}$,$\widehat{a}$的值($\widehat{b}$,$\widehat{a}$精确到0.01)与(I)中b,a的值差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井?(参考公式和计算结果:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\sum_{i=1}^{4}{{x}_{2i-1}}^{2}$=94,$\sum_{i=1}^{4}{x}_{2i-1}{y}_{2i-1}$=945)
(Ⅲ)设出油量与勘探深度的比值k不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数X的分布列与数学期望.
12.已知过抛物线y2=4x焦点F的直线l交抛物线于A、B两点(点A在第一象限),若$\overrightarrow{AF}$=3$\overrightarrow{FB}$,则直线l的方程为( )
| A. | x-2y-1=0 | B. | 2x-y-2=0 | C. | x-$\sqrt{3}$y-1=0 | D. | $\sqrt{3}$x-y-$\sqrt{3}$=0 |