若2是函数f(x)=x3-ax内任取一点x0.使lnx0＜0的概率是$\frac{1}{4}$．题目和参考答案——青夏教育精英家教网—

题目内容

12．若2是函数f（x）=x³-ax（a∈R）的零点，则在（0，a）内任取一点x₀，使lnx₀＜0的概率是$\frac{1}{4}$．

分析首先由零点求出a，然后求出满足lnx₀＜0的范围，利用几何概型的公式得到所求．

解答解：由题意，2是函数f（x）=x³-ax（a∈R）的零点，则a=4，在（0，4）内任取一点x₀，使lnx₀＜0的x₀∈（0，1），由几何概型的公式得到$\frac{1}{4}$；
故答案为：$\frac{1}{4}$

点评本题考查了几何概型的概率求法；关键是求出满足lnx₀＜0的范围没理由区间长度比求概率．

练习册系列答案

3．已知平面区域$Ω：\left\{{\begin{array}{l}{3x+4y-18≤0}\\{x≥2}\\{y≥0}\end{array}}\right.$，夹在两条斜率为$-\frac{3}{4}$的平行直线之间，且这两条平行直线间的最短距离为m．若点P（x，y）∈Ω，则z=mx-y的最小值为（　　）

20．

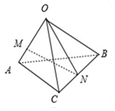如图，空间四边形OACB中，$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$，$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$，$\overrightarrow{{O}C}$=$\overrightarrow{c}$，点M在OA上，且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$，点N为BC中点，则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$．（用向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$表示）

7．设D，E，F分别△ABC的三边AB，BC，CA的中点，则$\overrightarrow{EA}+\overrightarrow{DC}$=（　　）

A．

$\overrightarrow{BC}$

B．

$3\overrightarrow{DF}$

C．

$\overrightarrow{BF}$

D．

$\frac{3}{2}\overrightarrow{BF}$

17．已知坐标原点O到直线$\sqrt{2}$ax+by-1=0（a，b∈R）的距离为$\frac{{\sqrt{2}}}{2}$，点Q（0，-1）在以点P（a，b）为圆心的圆P上，则圆P的最大半径是$\sqrt{2}$+1．

4．我国古代数学著作《九章算术》中有如下问题：“今有蒲生一日，长三尺，莞生一日，长一尺．蒲生日自半．莞生日自倍．问几何日而长等？”意思是“今有蒲草第一天长高3尺，菀草第一天长高1尺．以后蒲草每天长高前一天的一半，而菀草每天长高前一天的2倍，问多少天蒲草和菀草高度相同？”根据上述已知条件，可求得第2.6天，蒲草和菀草高度相同．（已知lg2=0.3010，lg3=0.4771，结果精确到0.1）

1．已知函数f（x）对任意x∈R都有f（x+6）+f（x）=2f（3），y=f（x-1）的图象关于点（1，0）对称，且f（4）=4，则f（2012）=（　　）

2．GZ新闻台做“一校一特色”访谈节目，分A，B，C三期播出，A期播出两间学校，B期，C期各播出1间学校，现从8间候选学校中选出4间参与这三项任务，不同的选法共有（　　）

试题分类