题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x>1}\\{1-{x}^{3},x≤1}\end{array}\right.$,若函数y=f(x)-a(x-1)恰有三个零点,则实数a的取值范围是( )| A. | (-$\frac{3}{4}$,0) | B. | (-∞,-$\frac{3}{4}$) | C. | (-3,-$\frac{3}{4}$) | D. | (0,1) |
分析 画出函数的图象,①当直线y=a(x-1)与曲线y=lnx相切于点(1,0)时,a=1,推出直线y=a(x-1)与函数f(x)的图象恰有3个交点时a的范围;②当直线y=a(x-1)与曲线y=1-x3相切时,设切点为(x0,1-x03),通过$\left\{\begin{array}{l}{a({x}_{0}-1)=1-{{x}_{0}}^{3}}\\{a=-3{{x}_{0}}^{2}}\end{array}\right.$,求出x0=1,a=-3或x0=-$\frac{1}{2}$,a=-$\frac{3}{4}$,然后判断求解a的范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{lnx,x>1}\\{1-{x}^{3},x≤1}\end{array}\right.$的图象如图所示,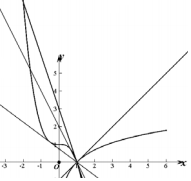
①当直线y=a(x-1)与曲线y=lnx相切于点(1,0)时,a=1,
故当a=0或a≥1时,直线y=a(x-1)与函数f(x)的图象恰有一个交点,
当0<a<1时,直线y=a(x-1)与函数f(x)的图象恰有两个交点,
②当直线y=a(x-1)与曲线y=1-x3相切时,设切点为(x0,1-x03),则$\left\{\begin{array}{l}{a({x}_{0}-1)=1-{{x}_{0}}^{3}}\\{a=-3{{x}_{0}}^{2}}\end{array}\right.$,
∴-3x02(x0-1)=1-x03,解得x0=1,a=-3或x0=-$\frac{1}{2}$,a=-$\frac{3}{4}$,
当-$\frac{3}{4}<a<0$时,直线y=a(x-1)与函数f(x)的图象恰有一个交点,
当a=-$\frac{3}{4}$或a≤-3时,直线y=a(x-1)与函数f(x)的图象恰有两个交点,
当-3<a<-$\frac{3}{4}$时,直线y=a(x-1)与函数f(x)的图象恰有三个交点,
故选:C.
点评 本题考查函数与方程的应用,考查数形结合以及转化思想的应用,考查计算能力.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 260 | B. | 250 | C. | 240 | D. | 230 |
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
(Ⅱ)据此判断是否有90%的把握认为选做《坐标系与参数方程》或《不等式选讲》与性别有关?
(Ⅲ)已知学习委员甲(女)和数学科代表乙(男)都选做《不等式选讲》.若在《不等式选讲》中按性别分层抽样抽取3人,记甲乙两人被选中的人数为,求的数学期望.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d.
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |