题目内容
8.在数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则a12+a22+a32+…+a102=( )| A. | (310-1)2 | B. | $\frac{{{9^{10}}-1}}{2}$ | C. | 910-1 | D. | $\frac{{{3^{10}}-1}}{4}$ |
分析 设Sn=a1+a2+a3+…+an=3n-1,n∈N*.利用递推关系可得:an=2×3n-1.再利用等比数列的前n项和公式即可得出.
解答 解:设Sn=a1+a2+a3+…+an=3n-1,n∈N*.
则n=1时,a1=2;当n≥2时,an=Sn-Sn-1=3n-1-(3n-1-1)=2×3n-1.
当n=1时,上式也成立,
∴an=2×3n-1.
∴${a}_{n}^{2}$=4×32n-2=4×9n-1,
∴数列$\{{a}_{n}^{2}\}$是等比数列,首项为4,公比为9.
∴a12+a22+a32+…+a102=$\frac{4({9}^{10}-1)}{9-1}$
=$\frac{{9}^{10}-1}{2}$.
故选:B.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19.设函数f(x)和g(x)分别是R上的偶函数和奇函数,则下列结论恒成立的是( )
| A. | |f(x)|-g(x)是奇函数 | B. | f(x)-|g(x)|是奇函数 | C. | |f(x)|+g(x)是偶函数 | D. | f(x)+|g(x)|是偶函数 |
13.在等差数列{an}中,a1=2,a2=$\frac{5}{2}$,则a4的值为( )
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | $\frac{1}{2}$ |
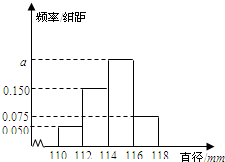 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.