题目内容
12. 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
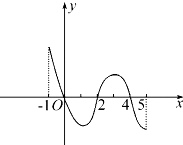
分析 由导数图象可知导函数的符号,从而可判断函数的单调性,得函数的极值即可.
解答 解:由导数图象可知,当-1<x<0或2<x<4时,f'(x)>0,函数单调递增,
当0<x<2或4<x<5,f'(x)<0,函数单调递减,
所以当x=0和x=4时,函数取得极大值f(0)=2,f(4)=2,
当x=2时,函数取得极小值f(2)=0,
所以f(x)的极小值为0,
故答案为:0.
点评 本题考查导数知识的运用,考查导函数与原函数图象之间的关系,正确运用导函数图象是关键.

练习册系列答案
相关题目
7.命题:“?x∈R,x2+mx+2≤0”为假命题,是命题|m-1|<2的( )
| A. | 充分不必要条件 | B. | 必要非充分条件 | C. | 充要条件 | D. | 都不是 |
1.命题“存在x0≥0,${2}^{{x}_{0}}$≤0”的否定是( )
| A. | 不存在x0≥0,${2}^{{x}_{0}}$>0 | B. | 存在x0≥0,${2}^{{x}_{0}}$≥0 | ||
| C. | 对任意的x0≥0,2x≤0 | D. | 对任意的x0≥0,2x>0 |
2.北京某小学组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有
且只有两个年级选择甲博物馆的方案有( )
且只有两个年级选择甲博物馆的方案有( )
| A. | A 6 2×A 5 4种 | B. | A 6 2×5 4种 | C. | C 6 2×A 5 4种 | D. | C 6 2×5 4 |
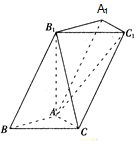 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.