题目内容
17．抛物线顶点在原点，以x轴为对称轴，过焦点且垂直于对称轴的弦长为8，求抛物线的方程．分析 设出抛物线方程，利用过焦点且垂直于对称轴的弦长为8，列出方程求解即可．
解答 解：设抛物线方程为y2=2ax（a≠0），则其焦点为$（{\frac{a}{2}，0}）$，将$\frac{a}{2}$代入y2=2ax得y=±a，
∴2|a|=8，a=±4，
所求抛物线方程为y2=±8x．
故答案为：y2=±8x．
点评 本题考查抛物线的简单性质的应用，抛物线方程的求法，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
3．命题p：方程$\frac{x^2}{m-5}-\frac{y^2}{m+3}=1$表示双曲线的充要条件是-3＜m＜5；
命题q：存在x0∈R，使得sinx0-cosx0=2，则（ ）
命题q：存在x0∈R，使得sinx0-cosx0=2，则（ ）
| A． | 命题“p或q”是假命题 | B． | 命题“p且q”是真命题 | ||
| C． | 命题“非q”是假命题 | D． | 命题“p且‘非q’”是真命题 |
12．
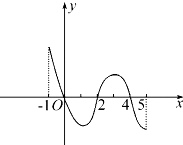已知函数f（x）的定义域为[-1，5]，部分对应值如表：
f（x）的导函数y=f′（x）的图象如图所示，则f（x）的极小值为0．
已知函数f（x）的定义域为[-1，5]，部分对应值如表：| x | -1 | 0 | 2 | 4 | 5 |
| f（x） | 1 | 2 | 0 | 2 | 1 |
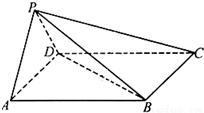如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，且PA=PD=$\frac{\sqrt{2}}{2}$AD．