题目内容
17.已知等比数列{an}的首项a1=1,公比为q,试就q的不同取值情况,讨论二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=3\\{a_2}x+{a_4}y=-2\end{array}\right.$何时无解,何时有无穷多解?分析 先消元,再根据等比数列的性质得到,0•x=3a4+2a3,问题得以解决.
解答 解:解方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=3\\{a_2}x+{a_4}y=-2\end{array}\right.$,消y得到(a1a4-a2a3)x=3a4+2a3,
∵等比数列{an}的公比为q,
∴a1a4-a2a3=0,
当3a4+2a3=0时,即q=-$\frac{2}{3}$时,方程组有无穷多解,
故选:C.
点评 本题以方程组的解为载体,考查等比数列的性质,属于基础题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.已知椭圆方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$的左、右焦点分别为F1,F2,过左焦点F1的直线交椭圆于A,B两点,则△ABF2的周长为( )
| A. | 12 | B. | 9 | C. | 6 | D. | 4 |
12.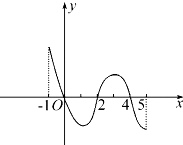 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:
f(x)的导函数y=f′(x)的图象如图所示,则f(x)的极小值为0.
 已知函数f(x)的定义域为[-1,5],部分对应值如表:
已知函数f(x)的定义域为[-1,5],部分对应值如表:| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 0 | 2 | 1 |
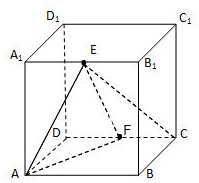 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点. 四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.
四棱锥P-ABCD中,底面ABCD是矩形,∠PCD=90°,二面角P-CD-B为60°,BC=1,AB=PC=2.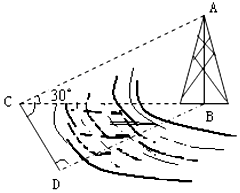 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与∠BCD=75°,∠BDC=60°,CD=20mD.现测得,并在点C测得塔顶A的仰角为30°,求塔高AB.