题目内容
7．命题：“?x∈R，x2+mx+2≤0”为假命题，是命题|m-1|＜2的（ ）| A． | 充分不必要条件 | B． | 必要非充分条件 | C． | 充要条件 | D． | 都不是 |
分析 分别求出命题：“?x∈R，x2+mx+2≤0”为假命题的m的范围，再求出命题|m-1|＜2的m的范围，根据集合的包含关系判断即可．
解答 解：若命题：“?x∈R，x2+mx+2≤0”为假命题，
则?x∈R，x2+mx+2＞0恒成立，
故△=m2-8＜0，解得：-2$\sqrt{2}$＜m＜2$\sqrt{2}$，
由|m-1|＜2，解得：-1＜m＜3，
故命题：“?x∈R，x2+mx+2≤0”为假命题是命题|m-1|＜2的既不充分也不必要条件，
故选：D．
点评 本题考查了充分必要条件，考查二次函数的性质以及绝对值不等式问题，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
四棱锥P-ABCD中，底面ABCD是矩形，∠PCD=90°，二面角P-CD-B为60°，BC=1，AB=PC=2．
13．已知点（x，y）满足$\left\{\begin{array}{l}x+2y-8≥0\\ 2x-y-6≤0\\ x-3y+7≥0\end{array}\right.$，则$z=\frac{x+1}{y-1}$的取值范围为（ ）
| A． | $[{\frac{3}{2}，5}]$ | B． | $[{\frac{2}{3}，5}]$ | C． | $[{\frac{3}{2}，7}]$ | D． | $[{\frac{2}{3}，7}]$ |
2．已知x∈（0，+∞）时，不等式9x-m•3x+m+1＞0恒成立，则m的取值范围是（ ）
| A． | 2-2$\sqrt{2}$＜m＜2+2$\sqrt{2}$ | B． | m＜2 | C． | m＜2+2$\sqrt{2}$ | D． | m$≥2+2\sqrt{2}$ |
12．
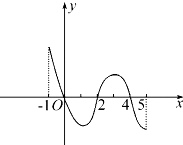已知函数f（x）的定义域为[-1，5]，部分对应值如表：
f（x）的导函数y=f′（x）的图象如图所示，则f（x）的极小值为0．
已知函数f（x）的定义域为[-1，5]，部分对应值如表：| x | -1 | 0 | 2 | 4 | 5 |
| f（x） | 1 | 2 | 0 | 2 | 1 |
17．曲线y=tanx在点（$\frac{π}{4}$，1）处的切线的斜率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | 1 | D． | 2 |