题目内容
已知在不等式组
(a≠1)所确定的平面区域中任意一点P(x,y),不等式x+y≤3恒成立,则z=2x-y的最小值为( )
|
| A、-1 | ||
| B、0 | ||
| C、3 | ||
D、2-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用不等式x+y≤3恒成立,确定a的取值范围,利用数形结合即可求出z=2x-y的最小值.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
要使不等式x+y≤3恒成立,则对应的平面区域在直线x+y=3的下方,
即A点在D点的下方即可.
当x=1时,y=3-x=3-1=2,即D(1,2),
当x=1时,1+ay=3,即ay=2,解得y=
,即A(1,
),
则满足0<
≤2,即a≥1,
∵a≠1,
∴a>1,
由z=2x-y,得y=2x-z,
平移直线y=2x,当直线y=2x经过点A时,直线y=2x-z的截距最大,此时z最小,
即最小值为z=2-
,
故选:D
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:要使不等式x+y≤3恒成立,则对应的平面区域在直线x+y=3的下方,
即A点在D点的下方即可.
当x=1时,y=3-x=3-1=2,即D(1,2),
当x=1时,1+ay=3,即ay=2,解得y=
| 2 |
| a |
| 2 |
| a |
则满足0<
| 2 |
| a |
∵a≠1,
∴a>1,
由z=2x-y,得y=2x-z,
平移直线y=2x,当直线y=2x经过点A时,直线y=2x-z的截距最大,此时z最小,
即最小值为z=2-
| 2 |
| a |
故选:D
点评:本题主要考查线性规划的应用,利用不等式恒成立确定a的取值范围是解决本题的关键,利用数形结合的思想即可得到结论.

练习册系列答案
相关题目
 已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )
已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
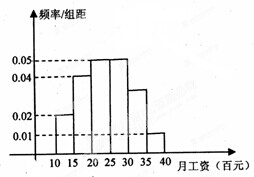 为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )
为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )| A、80 | B、150 |
| C、230 | D、400 |
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
| A、60种 | B、70种 |
| C、75种 | D、150种 |
