题目内容
已知复数z=
,
是z的共轭复数,则z•
=( )
| 4 | ||
1+
|
. |
| z |
. |
| z |
| A、4 | B、3 | C、2 | D、1 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:由条件利用两个复数代数形式的乘除法,虚数单位i的幂运算性质,求得z的值,可得
,从而求得z•
的值.
. |
| z |
. |
| z |
解答:
解:∵复数z=
=
=1-
i,∴
=1+
i,
∴z•
=(1-
i)(1+
i)=4,
故选:A.
| 4 | ||
1+
|
4(1-
| ||||
(1+
|
| 3 |
. |
| z |
| 3 |
∴z•
. |
| z |
| 3 |
| 3 |
故选:A.
点评:本题主要考查复数基本概念,两个复数代数形式的乘除法,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
已知a,b∈R,则“log2a>log2b”是“a>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“点M(a,b)在函数y=log2x的图象上”是“点N(a4,4b)在函数y=log2x的图象上”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
定义在R上的函数满足f(x+2)=f(x),且x∈[1,3]时,f(x)=cos
x,则下列大小关系正确的是( )
| π |
| 2 |
A、f(tan1)>f(
| ||||
B、f(cos
| ||||
| C、f(sin2)>f(cos2) | ||||
| D、f(cos1)>f(sin1) |
已知a=sin
sin
,b=cos2
,c=cos
-sin
,则( )
| π |
| 8 |
| 5π |
| 8 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| A、a<c<b |
| B、a<b<c |
| C、b<a<c |
| D、c<a<b |
执行如图所示的程序框图,若输入x∈[0,2π],则输出y的取值范围是( )


| A、[0,1] | ||||
| B、[-1,1] | ||||
C、[-
| ||||
D、[-1,
|
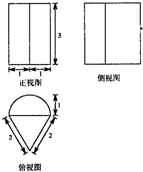
某几何体的三视图如图所示,则该几何体的体积等于( )

A、
| ||||
B、3(
| ||||
C、3(
| ||||
D、
|
已知函数f(x)=sin2x-
cos2x的图象向左平移m(m>0)个单位后关于y轴对称,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|