题目内容
对于数列{an},有a0=1,ai∈[0,
],tanan=
,求a100.
| π |
| 2 |
| ||
| tanan-1 |
考点:数列与三角函数的综合
专题:等差数列与等比数列,三角函数的求值
分析:由数列递推式结合同角三角函数的基本关系式得到an=
an-1,再由已知a0=1求得a1,则a100可求.
| 1 |
| 2 |
解答:
解:tanan=
=
=
=
=
=tan
.
∵ai∈[0,
],∴an=
an-1.
a0=1,a1=
,
则a100=(
)100.
| ||
| tanan-1 |
=
| ||
| tanan-1 |
| ||
| tanan-1 |
| ||
|
| 1-cosan-1 |
| sinan-1 |
| an-1 |
| 2 |
∵ai∈[0,
| π |
| 2 |
| 1 |
| 2 |
a0=1,a1=
| 1 |
| 2 |
则a100=(
| 1 |
| 2 |
点评:本题考查了数列与三角的综合,考查了同角三角函数的基本关系式,考查了等比数列的通项公式,是中档题.

练习册系列答案
相关题目
y=
-log2(4-x2)的定义域是( )
|
| A、(-2,0)∪(1,2) |
| B、(-2,0]∪(1,2) |
| C、(-2,0)∪[1,2) |
| D、[-2,0]∪[1,2] |
在实数集上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x都成立,则实数a的取值范围是( )
A、(-
| ||||
| B、(0,2) | ||||
| C、(-1,1) | ||||
D、(-
|
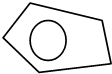 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )| A、4π | B、5π | C、6π | D、7π |