题目内容

在实数集上定义运算?：x?y=x（1-y），若不等式（x-a）?（x+a）＜1对任意实数x都成立，则实数a的取值范围是（　　）
A、(-
1
2
，
3
2
)
B、（0，2）
C、（-1，1）
D、(-
3
2
，
1
2
)
考点：二次函数的性质
专题：函数的性质及应用
分析：根据定义将不等式进行转化，解不等式即可．
解答： 解：由定义不等式等价为（x-a）?（x+a）=（x-a）[1-（x+a）]=-x2+x+a2-a＜1对任意实数x都成立，
即x2-x-a2+a+1＞0恒成立，
则△＜0，
即1-4（-a2+a+1）=4a2-4a-3＜0，
解得-
1
2
＜a＜
3
2
，
故选：A．
点评：本题考查了在新定义下对函数恒成立问题的应用．利用一元二次不等式的解法是解决本题的关键．关于新定义型的题，关键是理解定义，并会用定义来解题．
练习册系列答案
相关题目
复数z=
-3+i
2+i
的共轭复数是（　　）
A、-1-iB、2-i
C、-1+iD、2+i
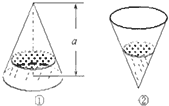如图①，一个圆锥形容器的高为a=2，内装有高度为h的一定量的水，如果将容器倒置，这时水所形成的圆锥的高恰为1（如图②），则图①中的水面高度h=
 
．
已知命题p：x1和x2是方程x2-mx-2=0的两个实根，不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1，1]恒成立；命题q：不等式ax2+2x-1＞0有解；若命题p是真命题，命题q是假命题，则a的取值范围为
 
．
对于数列{an}，有a0=1，ai∈[0，
π
2
]，tanan=
1+tan2an-1
-1
tanan-1
，求a100．
已知中心在坐标原点，对称轴为坐标轴的双曲线有一条渐近线方程为2x-3y=0，则该双曲线的离心率为
 
．
若双曲线
x2
a2
-
y2
16
=1（a＞0）的焦点为F1（-5，0），F2（5，0），则双曲线的离心率为（　　）
A、
4
3
B、
5
3
C、2
D、
2
已知函数f（x）=x2+ax-lnx，a∈R．
（1）若a=1，求函数f（x）的单调区间；
（2）令g（x）=f（x）-x2，是否存在实数a，当x∈（0，e]（e是自然常数）时，函数g（x）的最小值是3，若存在，求出a的值；若不存在，说明理由．
（3）求证：当x∈（0，e]时，e2x-
5
2
＞lnx+
lnx
x
．
设x，y∈R，向量
a
=（x，1），
b
=（1，y），
c
=（2，-4），且
a
⊥
c
，
b
∥
c
，则|
a
+
b
+
c
|=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网