题目内容
2.对任意的正整数n,以及任意n个互不相同的正整数a1,a2,…,an,若不等式${({\frac{1}{a_1}})^λ}+{({\frac{1}{a_2}})^λ}+…+{({\frac{1}{a_n}})^λ}<2$恒成立,求整数λ的最小值.分析 由$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}$>2,讨论若λ≤1,则有$(\frac{1}{1})^{λ}+(\frac{1}{2})^{λ}+(\frac{1}{3})^{λ}+(\frac{1}{4})^{λ}$≥1$+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$>2,与题意不符;可得λ>1;当λ≥2时,由a1,a2,…,an为n个互不相同的正整数值,可得$(\frac{1}{{a}_{1}})^{λ}+(\frac{1}{{a}_{2}})^{λ}+…+(\frac{1}{{a}_{n}})^{λ}$≤$(\frac{1}{1})^{λ}+(\frac{1}{2})^{λ}+(\frac{1}{3})^{λ}+…+(\frac{1}{n})^{λ}$≤$(\frac{1}{1})^{2}+(\frac{1}{2})^{2}+(\frac{1}{3})^{2}+…+(\frac{1}{n})^{2}$,利用裂项相消法可得$(\frac{1}{{a}_{1}})^{λ}+(\frac{1}{{a}_{2}})^{λ}+…+(\frac{1}{{a}_{n}})^{λ}$=2-$\frac{1}{n}$<2.由此求得整数λ的最小值为2.
解答 解:∵$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}$>2,
∴若λ≤1,则有$(\frac{1}{1})^{λ}+(\frac{1}{2})^{λ}+(\frac{1}{3})^{λ}+(\frac{1}{4})^{λ}$≥1$+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$>2,与题意不符;
∴λ>1,
当λ≥2时,由a1,a2,…,an为n个互不相同的正整数值,
∴$(\frac{1}{{a}_{1}})^{λ}+(\frac{1}{{a}_{2}})^{λ}+…+(\frac{1}{{a}_{n}})^{λ}$≤$(\frac{1}{1})^{λ}+(\frac{1}{2})^{λ}+(\frac{1}{3})^{λ}+…+(\frac{1}{n})^{λ}$≤$(\frac{1}{1})^{2}+(\frac{1}{2})^{2}+(\frac{1}{3})^{2}+…+(\frac{1}{n})^{2}$
$≤1+\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{(n-1)n}$=$1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n-1}-\frac{1}{n}$=2-$\frac{1}{n}$<2.
∴当λ≥2时,不等式${({\frac{1}{a_1}})^λ}+{({\frac{1}{a_2}})^λ}+…+{({\frac{1}{a_n}})^λ}<2$对任意n个互不相同的正整数a1,a2,…,an恒成立,
∴整数λ的最小值为2.
点评 本题考查恒成立问题,考查数学转化思想方法和分类讨论的数学思想方法,训练了利用裂项相消法求数列的和,是中档题.

| A. | 6 | B. | 5 | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
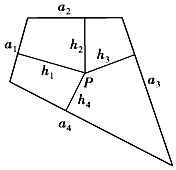 如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )
如图所示,面积为S的平面凸四边形的第i条边的边长为ai(i=1,2,3,4),此四边形内在一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k,则h1+3h2+5h3+7h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K,H1+3H2+5H3+7H4=( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{3V}{K}$ | D. | $\frac{V}{3K}$ |
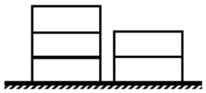 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).