题目内容
13.已知△ABC的面积为S,且$\overrightarrow{AB}•\overrightarrow{AC}=S$.(1)求sinA,cosA,tan2A的值;
(2)若$B=\frac{π}{4},\;\;|{\overrightarrow{CA}-\overrightarrow{CB}}|=6$,求△ABC的面积S.
分析 (1)把S=$\frac{1}{2}bcsinA$代入$\overrightarrow{AB}•\overrightarrow{AC}=S$,解出A,
(2)c=|$\overrightarrow{BA}$|=|$\overrightarrow{CA}-\overrightarrow{CB}$|=6,求出sinC,使用正弦定理求出b,代入面积公式.
解答 解:(1)∵$\overrightarrow{AB}•\overrightarrow{AC}=S$,∴b•c•cosA=$\frac{1}{2}$bcsinA,∴tanA=2,A∈(0,$\frac{π}{2}$).
∵sin2A+cos2A=1,∴sinA=$\frac{2\sqrt{5}}{5}$,cosA=$\frac{\sqrt{5}}{5}$,tan2A=$\frac{2tanA}{1-ta{n}^{2}A}$=$-\frac{4}{3}$.
(2)|$\overrightarrow{BA}$|=|$\overrightarrow{CA}-\overrightarrow{CB}$|=6,即c=6.sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{2\sqrt{5}}{5}×\frac{\sqrt{2}}{2}+\frac{\sqrt{5}}{5}×\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{10}}{10}$.
由正弦定理得:$\frac{b}{sinB}=\frac{c}{sinC}$,∴b=$\frac{c•sinB}{sinC}$=2$\sqrt{5}$.
∴S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×2\sqrt{5}×6×\frac{2\sqrt{5}}{5}$=12.
点评 本题考查了平面向量在解三角形中的应用,属于中档题.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | (-1,0) | B. | [-2,0] | C. | (-∞,-2)∪(-1,0) | D. | [-2,+∞) |
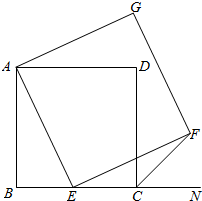 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.