题目内容
20.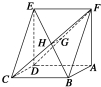 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4,求四棱锥F-ABCD的体积.
分析 (1)方法一:推导出四边形EFBC是平行四边形,从而HG∥CD,由此能证明GH∥平面CDE.
方法二:连接EA,推导出GH∥CD,由此能证明GH∥平面CDE.
(2)推导出FA⊥平面ABCD,BD⊥CD.由此能求出四棱锥F-ABCD的体积VF-ABCD.
解答 证明:(1)方法一:∵EF∥AD,AD∥BC,∴EF∥BC.
又EF=AD=BC,∴四边形EFBC是平行四边形,…(3分)
∴H为FC的中点.又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.…(6分)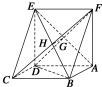 方法二 连接EA,∵ADEF是正方形,
方法二 连接EA,∵ADEF是正方形,
∴G是AE的中点.
∴在△EAB中,GH∥AB.…(3分)
又∵AB∥CD,∴GH∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.…(6分)
解:(2)∵平面ADEF⊥平面ABCD,交线为AD,
且FA⊥AD,∴FA⊥平面ABCD.…(9分)
∵AD=BC=6,∴FA=AD=6.
又∵CD=2,DB=4,CD2+DB2=BC2,∴BD⊥CD.
∵S?ABCD=CD•BD=8,
∴VF-ABCD=$\frac{1}{3}$S?ABCD•FA=$\frac{1}{3}×$8×6=16.…(12分)
点评 本题考查线面平行的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知△ABC中,sinA+cosA=$\frac{7}{13}$,则cosA等于( )
| A. | $\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
8.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线,则关于x的方程$\overrightarrow{a}$x2+$\overrightarrow{b}$x+$\overrightarrow{c}$=0的解的情况是( )
| A. | 至少有一个实数解 | B. | 至多只有一个实数解 | ||
| C. | 至多有两个实数解 | D. | 可能有无数个实数解 |