题目内容
10.设数列{an}使得a1=0,且对任意的n∈N*,均有|an+1-an|=n,则a3所有可能的取值构成的集合为{-3,-1,1,3};a64的最大值为2016.分析 ①由于a1=0,且对任意的n∈N*,均有|an+1-an|=n,则n=1时,|a2-0|=1,解得a2=±1.利用|a3-a2|=2,即可得出a3.
②对任意的n∈N*,均有|an+1-an|=n,可得:an+1-an=±n,取an+1-an=n,a1=0时,数列{an}单调递增,利用“累加求和”方法即可得出.
解答 解:①∵a1=0,且对任意的n∈N*,均有|an+1-an|=n,
∴n=1时,|a2-0|=1,解得a2=±1.
∴a2=1,则|a3-1|=2,解得a3=3,-1.
∴a2=-1,则|a3+1|=2,解得a3=-3,1.
∴a3所有可能的取值构成的集合为{-3,-1,1,3}.
②对任意的n∈N*,均有|an+1-an|=n,可得:an+1-an=±n,
取an+1-an=n,a1=0时,数列{an}单调递增,
可得:an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-1)+(n-2)+…+1+0
=$\frac{n(n-1)}{2}$,
则a64的最大值=$\frac{64×63}{2}$=2016.
故答案为:{-3,-1,1,3},2016.
点评 本题考查了数列递推关系、等差数列的通项公式、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.椭圆x2+4y2=16的长轴长和短轴长依次为( )
| A. | 4,2 | B. | 8,4 | C. | 4,2$\sqrt{3}$ | D. | 8,4$\sqrt{3}$ |
15.下列各图形中,不可能是某函数y=f(x)的图象的是( )
| A. |  | B. |  | C. |  | D. |  y |
2.若4sinα-3cosα=0,则$\frac{1}{{{{cos}^2}α+2sin2α}}$的值为( )
| A. | $\frac{25}{16}$ | B. | 1 | C. | $\frac{25}{48}$ | D. | $\frac{25}{64}$ |
20.函数$f(x)={x^2}+\frac{1}{|x|}$的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
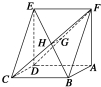 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.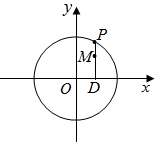 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.