已知△ABC中.sinA+cosA=$\frac{7}{13}$.则cosA等于( )A．$\frac{12}{13}$B．$\frac{5}{13}$C．-$\frac{5}{13}$D．-$\frac{12}{13}$ 题目和参考答案——青夏教育精英家教网—

题目内容

11．已知△ABC中，sinA+cosA=$\frac{7}{13}$，则cosA等于（　　）

A．

$\frac{12}{13}$

B．

$\frac{5}{13}$

C．

-$\frac{5}{13}$

D．

-$\frac{12}{13}$

分析由条件利用同角三角函数的基本关系，求得cosA的值．

解答解：△ABC中，∵sinA+cosA=$\frac{7}{13}$，∴sinAcosA=-$\frac{60}{169}$，
则cosA＜0，解得cosA=-$\frac{5}{13}$，
故选：C．

点评本题主要考查同角三角函数的基本关系，属于基础题．

练习册系列答案

$\frac{{3\sqrt{2}}}{2}$

D．

2．已知函数f（x）=$\frac{{x}^{2}}{2}$-alnx（a＞0）在[1，2]上为单调函数，则a的取值范围为（　　）

19．已知数列{a_n}的首项a₁=1且a_n=-$\frac{1}{2}$a_n-1（n≥2），则a₄等于（　　）

6．根据下列条件，写出数列的前4项，并归纳猜想它的通项公式（不需证明）．
（1）a₁=0，a_n+1=$\frac{1}{2-{a}_{n}}$；
（2）对一切的n∈N^*，a_n＞0，且2$\sqrt{{S}_{n}}$=a_n+1．

16．对于回归方程$\widehat{y}$=4.75x+257，当x=28时，y的估计值为（　　）

3．实数a，b，c，d满足|b-a+4|+（c+d²-3lnd）²=0，则（b-d）²+（a-c）²的最小值是18．

20．

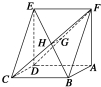如图，已知平行四边形ABCD中，BC=6，正方形ADEF所在平面与平面ABCD垂直，G，H分别是DF，BE的中点．
（1）求证：GH∥平面CDE；
（2）若CD=2，DB=4，求四棱锥F-ABCD的体积．

1．化简或计算下列各式：
（1）16${\;}^{-\frac{1}{2}}}$-（${\frac{1}{2}}$）${\;}^{-\frac{1}{2}}}$-（${\frac{27}{8}}$）${\;}^{\frac{2}{3}}}$+（${\frac{3}{5}}$）⁰+$\root{4}{{{{（1-\sqrt{2}）}^4}}}$；
（2）（a${\;}^{\frac{2}{3}}}$b${\;}^{\frac{1}{2}}}$）×（-3a${\;}^{\frac{1}{2}}}$b${\;}^{\frac{1}{3}}}$）÷（$\frac{1}{3}$a${\;}^{\frac{1}{6}}}$b${\;}^{\frac{5}{6}}}$）．

试题分类