题目内容
2.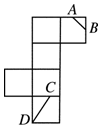 如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )
如图所示,是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )| A. | $\frac{{\sqrt{2}}}{5}$ | B. | $\frac{{\sqrt{3}}}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
分析 正方体的表面展开图还原成正方体,能求出异面直线AB和CD的夹角的余弦值.
解答 解:正方体的表面展开图还原成正方体,如图,
则异面直线AB和CD所成角为∠EFG,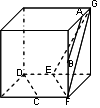
设正方体棱长为2,
在△EFG中,EF=DC=$\sqrt{5}$,EG=$\sqrt{5}$,FG=2$\sqrt{2}$,
∴cos∠EFG=$\frac{\frac{1}{2}FG}{EF}$=$\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$.
∴异面直线AB和CD的夹角的余弦值为$\frac{\sqrt{10}}{5}$.
故选:C.
点评 本题考查异面直线的夹角的余弦值的求法,是中档题,解题时要认真审题,注意正方体的结构特征的合理运用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
12.已知集合A={x|y=x2},集合B={y|y=x2},则∁AB等于( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
13.向量$\overrightarrow b=(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,则向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
7.△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若BC=m,∠B=α,则AD长为( )
| A. | msin2α | B. | mcos2α | C. | msinαcosα | D. | msinαtanα |
14.圆x2+y2+4x-1=0关于原点O对称的圆的方程为( )
| A. | (x-2)2+y2=5 | B. | x2+(y-2)2=5 | C. | (x+2)2+(y+2)2=5 | D. | x2+(y+2)2=5 |
3.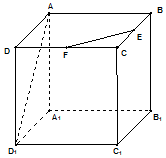 如图,在正方体ABCD-A1B1C1D1中,AA1=a,E,F分别是BC,DC的中点,则异面直线AD1与EF所成角为( )
如图,在正方体ABCD-A1B1C1D1中,AA1=a,E,F分别是BC,DC的中点,则异面直线AD1与EF所成角为( )
 如图,在正方体ABCD-A1B1C1D1中,AA1=a,E,F分别是BC,DC的中点,则异面直线AD1与EF所成角为( )
如图,在正方体ABCD-A1B1C1D1中,AA1=a,E,F分别是BC,DC的中点,则异面直线AD1与EF所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |