题目内容
已知凼数F(x)为二次凼数,且F(x)的导凼数为f(x),若存在实数a∈(-2,-1),使f(-a)=-f(a)>0,则不等式F(2x-1)>F(x)的解集为( )
A、{x|x<
| ||
B、{x|x<
| ||
C、{x|
| ||
D、{x|x<-1或x>-
|
考点:二次函数的性质
专题:函数的性质及应用
分析:根据F(x)的导函数f(x)是一次函数,且a∈(-2,-1)时,f(-a)=-f(a)>0,
求出F(x)的解析式,再把不等式F(2x-1)>F(x)转化为普通不等式,求出解集即可.
求出F(x)的解析式,再把不等式F(2x-1)>F(x)转化为普通不等式,求出解集即可.
解答:
解:∵F(x)为二次函数,∴F(x)的导函数f(x)是一次函数;
不妨设f(x)=2kx+b,(k≠0);
又存在实数a∈(-2,-1),使f(-a)=-f(a)>0,
∴2k(-a)+b=-(2ka+b),
∴b=0;
∴-2ka>0,
∴ka<0,
∴k>0;
∴F(x)=kx2+c,(k>0);
∴不等式F(2x-1)>F(x)可化为
k(2x-1)2+c>kx2+c,
化简得(2x-1)2>x2,
即(3x-1)(x-1)>0,
解得x<
或x>1;
∴该不等式的解集为{x|x<
或x>1}.
故选:B.
不妨设f(x)=2kx+b,(k≠0);
又存在实数a∈(-2,-1),使f(-a)=-f(a)>0,
∴2k(-a)+b=-(2ka+b),
∴b=0;
∴-2ka>0,
∴ka<0,
∴k>0;
∴F(x)=kx2+c,(k>0);
∴不等式F(2x-1)>F(x)可化为
k(2x-1)2+c>kx2+c,
化简得(2x-1)2>x2,
即(3x-1)(x-1)>0,
解得x<
| 1 |
| 3 |
∴该不等式的解集为{x|x<
| 1 |
| 3 |
故选:B.
点评:本题考查了二次函数的性质与应用的问题,也考查了导数的概念与应用问题,是基础题目.

练习册系列答案
相关题目
已知四个函数f(x)=sin(sinx),g(x)=sin(cosx),h(x)=cos(sinx),φ(x)=cos(cosx)在x∈[-π,π]上的图象如图,则函数与序号匹配正确的是( )

| A、f(x)-①,g(x)-②,h(x)-③,φ(x)-④ |
| B、f(x)-①,φ(x)-②,g(x)-③,h(x)-④ |
| C、g(x)-①,h(x)-②,f(x)-③,φ(x)-④ |
| D、f(x)-①,h(x)-②,g(x)-③,φ(x)-④ |
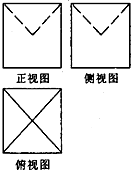 某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
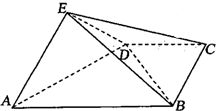 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
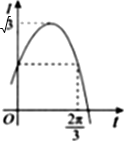
 已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<
已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<