题目内容
已知函数f(x)=
sin(2x-
)+2sin2(x-
)(x∈R)
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)取得最大值时的x集合;
(3)函数f(x)的图象可以由函数y=sinx(x∈R)的图象经过怎样的变换得到?
| 3 |
| π |
| 6 |
| π |
| 12 |
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)取得最大值时的x集合;
(3)函数f(x)的图象可以由函数y=sinx(x∈R)的图象经过怎样的变换得到?
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先通过三角函数的恒等变换把函数关系式变形成正弦型函数,进一步求出函数的单调区间.
(2)直接利用整体思想求出函数的最值和单调区间.
(3)利用正弦函数的变换规律求出结果.
(2)直接利用整体思想求出函数的最值和单调区间.
(3)利用正弦函数的变换规律求出结果.
解答:
解:(1)f(x)=
sin(2x-
)+2sin2(x-
)
=
sin(2x-
)-cos(2x-
)+1,
=2sin(2x-
)+1,
所以:f(x)=2sin(2x-
)+1,
令:-
+2kπ≤2x-
≤2kπ+
,
解得:-
+kπ≤x≤kπ+
,
所以单调递增区间为[kπ-
,kπ+
],k∈Z,
(2)令:2x-
=2kπ+
,
函数f(x)取得最大值的x集合为:
{x|x=kπ+
,k∈Z},
(3)先将函数y=sinx的图象向右平移
个单位;再纵坐标不变,横坐标缩小为原来的
倍; 再横坐标不变,纵坐标扩大为原来的2倍;最后整个图象向上平移1个单位.或者先将函数y=sinx的图象纵坐标不变,横坐标缩小为原来的
倍;再将图象向右平移
个单位;再横坐标不变,纵坐标扩大为原来的2倍;最后整个图象向上平移1个单位.
| 3 |
| π |
| 6 |
| π |
| 12 |
=
| 3 |
| π |
| 6 |
| π |
| 6 |
=2sin(2x-
| π |
| 3 |
所以:f(x)=2sin(2x-
| π |
| 3 |
令:-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得:-
| π |
| 12 |
| 5π |
| 12 |
所以单调递增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
(2)令:2x-
| π |
| 3 |
| π |
| 2 |
函数f(x)取得最大值的x集合为:
{x|x=kπ+
| 5π |
| 12 |
(3)先将函数y=sinx的图象向右平移
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,正弦型函数的单调区间的确定,函数图象得变换问题.属于基础题型.

练习册系列答案
相关题目
在△ABC中,AB=4,∠ABC=30°,D是边BC上的一点,且
•
=
•
,则
•
的值为( )
| AD |
| AB |
| AD |
| AC |
| AD |
| AB |
| A、0 | B、4 | C、8 | D、-4 |
已知四个函数f(x)=sin(sinx),g(x)=sin(cosx),h(x)=cos(sinx),φ(x)=cos(cosx)在x∈[-π,π]上的图象如图,则函数与序号匹配正确的是( )

| A、f(x)-①,g(x)-②,h(x)-③,φ(x)-④ |
| B、f(x)-①,φ(x)-②,g(x)-③,h(x)-④ |
| C、g(x)-①,h(x)-②,f(x)-③,φ(x)-④ |
| D、f(x)-①,h(x)-②,g(x)-③,φ(x)-④ |
已知F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,若点M在以线段F1F2为直径的圆外,则双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(
| ||
| D、(2,+∞) |
 已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<
已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<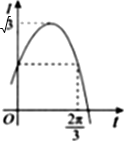
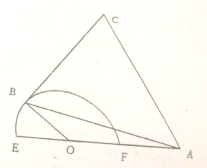 如图,AO=2,B是半个单位圆上的动点,△ABC是等边三角形,求当∠AOB等于多少时,四边形OACB的面积最大,并求四边形面积的最大值.
如图,AO=2,B是半个单位圆上的动点,△ABC是等边三角形,求当∠AOB等于多少时,四边形OACB的面积最大,并求四边形面积的最大值.