题目内容

将正奇数按下列规律排列，则第21行从左向右的第5个数为（　　）
1
3　5　7
9　11　13　15　17
19　21　23　25　27　29　31
…
A、811B、809
C、807D、805
考点：归纳推理
专题：规律型,等差数列与等比数列
分析：第一行有1个奇数，第二行有2个奇数，…第n行有n个奇数，每行的最后的奇数是第1+2+3+…+n=（1+n）×n÷2个奇数，这个奇数是2×（1+n）×n÷2-1=（1+n）×n-1，这就是行数n和这行的最后一个奇数的关系，依照这个关系，可得答案．
解答： 解：由题意知前20行共有正奇数1+3+5+…+39=202=400个，
则第21行从左向右的第5个数是第405个正奇数，
所以这个数是2×405-1=809．
故选：B
点评：本题从观察数阵的排列规律，考查了数列的求和应用问题；解题时，关键是发现规律并应用所学知识，来解答问题．
练习册系列答案
相关题目
①由“若a，b，c∈R，则（ab）c=a（bc）”类比“若
a
、
b
、
c
为三个向量，则（
a
•
b
）
c
=
a
（
b
•
c
）”；
②在数列{an}中，a1=0，an+1=2an+2，猜想an=2n-2；
③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”；上述三个推理中；
正确的个数为（　　）
A、0B、1C、2D、3
设函数f（x）=
4sinθ
3
x3+
3
cosθx2+sinθ，其中θ∈[0，
5π
12
]，则导数f′（
1
2
）的取值范围是（　　）
A、[-2，2]
B、[
2
，
3
]
C、[
3
，2]
D、[
2
，2]
下列说法正确的有几个（　　）
（1）回归直线过样本点的中心（
.
x
，
.
y
）；
（2）线性回归方程对应的直线
∧
y
=
∧
b
x+
∧
a
至少经过其样本数据点（x1，y1），（x2，y2），…，（xn，yn）中的一个点；
（3）在残差图中，残差点分布的带状区域的宽度越宽，其模型拟合的精度越高；
（4）在回归分析中，R2为0.98的模型比R2为0.80的模型拟合的效果好．
A、1B、2C、3D、4
已知椭圆
x2
3m2
+
y2
n2
=1和双曲线
x2
2m2
-
y2
3n2
=1有公共焦点，那么双曲线的离心率为（　　）
A、
5
4
B、
22
2
C、
22
4
D、3
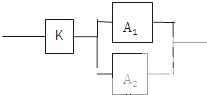如图．用K，A1，A2分别不同的原件连接成一个系统．当K正常工作且A1和A2正常工作的概率是0.9，0.8，0.8则系统正常工作的概率为（　　）
A、0.960B、0.864
C、0.72D、0.576
若f′（x0）=-3，则
lim
h→0
f(x0+h)-f(x0-3h)
h
=（　　）
A、-3B、-12C、-9D、-6
定义在（0，+∞）上的可导函数f（x）满足：xf′（x）+f（x）＜0且f（1）=1，则不等式xf（x）＞1的解集为（　　）
A、（-∞，1）
B、（0，1）
C、（1，+∞）
D、（0，1]
设函数f（x）=cos（2x+
π
3
）+
3
sin2x+2a
（1）求函数f（x）的单调递增区间
（2）当0≤x≤
π
4
时，f（x）的最小值为0，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网