��Ŀ����
1����ֱ֪��l�IJ�������Ϊ$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$��tΪ������������ԭ��OΪ���㣬��x��������Ϊ���ᣬ����������ϵ������C�ķ���Ϊ$sin��-\sqrt{3}��{cos^2}��=0$������������C��ֱ�����귽�̣�
����д��ֱ��l������C�����һ�������꣮
���� �������ü�������ֱ�����껥��������������C��ֱ�����귽�̣�
����$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$������$y-\sqrt{3}{x^2}=0$�ã�$\sqrt{3}+\sqrt{3}t-\sqrt{3}{��{1+\frac{1}{2}t}��^2}=0$������������꣬����ֱ��l������C�����һ�������꣮
��� �⣺����$sin��-\sqrt{3}��{cos^2}��=0$����$��sin��-\sqrt{3}{��^2}{cos^2}��=0$��
��$y-\sqrt{3}{x^2}=0$��
����$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=\sqrt{3}+\sqrt{3}t\end{array}\right.$������$y-\sqrt{3}{x^2}=0$�ã�$\sqrt{3}+\sqrt{3}t-\sqrt{3}{��{1+\frac{1}{2}t}��^2}=0$����t=0��
�Ӷ�����������Ϊ$��{1��\sqrt{3}}��$��
���ԣ������һ��������Ϊ$��{2��\frac{��}{3}}��$��
���� ���⿼�鼫������ֱ�����껥��������������̵����ã��Ƚϻ�����

��ϰ��ϵ�д�
 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
�����Ŀ
11�� �ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������
�ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������
 �ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������
�ؾ������ҹ�����ʱ�ڵ���ѧ�ң����ݣ����Ĵ�ʡ�����أ��ˣ����������ġ�������¡�������Ķ���ʽ��ֵ���ؾ����㷨���������DZȽ��Ƚ����㷨����ͼ��ʾ�ij����ͼ�����������ؾ����㷨��ij����ʽֵ��һ��ʵ����������x��ֵΪ2�������v��ֵΪ��������| A�� | 210-1 | B�� | 210 | C�� | 310-1 | D�� | 310 |
12��������R�ϵ�ż����f��x���ĵ�����Ϊf'��x�������������ʵ��x������2f��x��+xf'��x����2���������ʹx2f��x��-4f��2����x2-4������ʵ��x��ȡֵ��Χ�ǣ�������
| A�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | B�� | ��-2��0���ȣ�0��2�� | C�� | {x|x�١�2} | D�� | ��-2��2�� |
9��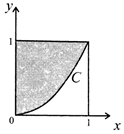 ����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������
����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������
 ����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������
����ͼ��ʾ�������������Ͷ��10000���㣬��������Ӱ���֣�����C�ķ���Ϊx2-y=0���ĵ�ĸ����Ĺ���ֵΪ��������| A�� | 5000 | B�� | 6667 | C�� | 7500 | D�� | 7854 |
6����x0�Ƿ���lnx+x-3=0��ʵ���⣬��x0�������䣨������
| A�� | ��1��1.5�� | B�� | ��1.5��2�� | C�� | ��2��2.5�� | D�� | ��2.5��3�� |
13����֪����$f��x��=\left\{\begin{array}{l}{3^{|x-1|}}��x��0\\-{x^2}-2x+1��x��0\end{array}\right.$��������x�ķ���f2��x��+��a-1��f��x��-a=0��7�����ȵ�ʵ��������ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | [1��2] | B�� | ��1��2�� | C�� | ��-2��-1�� | D�� | [-2��-1] |
11����֪����A={x|2x2+x-3=0}������B={i|i2��4}}��∁RC={-1��1��$\frac{3}{2}$}����A��BU∁RC=��������
| A�� | {1��-1��$\frac{3}{2}$} | B�� | {-2��1��-$\frac{3}{2}$��-1} | C�� | {1} | D�� | {2��1��-1��$\frac{3}{2}$} |